
����Ŀ��ij�н������Ϣ������ҵ���ԣ�����ѧ����ǩ�ķ�ʽ�����Լ��Ŀ������ݣ��涨��ÿλ�����������������⣨��ǩ�ֱ��ô���B1��B2��B3��ʾ���г�ȡһ�������������ϻ��⣨��ǩ�ֱ��ô���J1��J2��J3��ʾ���г�ȡһ�����п��ԣ�С���ڿ�������ǩ������£��ֱ�ӱ�������ϻ���������س�ȡһ����ǩ��
��1������״ͼ���б�����ʾ�����п��ܵĽ����
��2����С���鵽�ı�������ϻ������ǩ������±꣨���硰B1�����±�Ϊ��1����Ϊһ������һ��ż���ĸ��ʣ�
���𰸡�
��1���⣺����״ͼ��

����9�ֵȿ��ܵĽ��
��2���⣺������״ͼ�����֪�����п��ܵĽ������9�֣����б�������ϻ������ǩ�����±�Ϊһ��һż����4�֣�
����ǩ�����±�Ϊһ��һż�ĸ����� ![]()
����������1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ������2���ɣ�1���е���״ͼ�����С���鵽�ı�������ϻ������ǩ������±꣨���硰B1�����±�Ϊ��1����Ϊһ������һ��ż���������Ȼ��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A��ʾ��������Ϊ��6����B��ʾ��������Ϊ6����P�ӵ�A������ÿ��4����λ���ȵ��ٶ�����������A��B�˶�������P�����B���������أ���Ȼ��ÿ��4����λ���ȵ��ٶ��˶�����Aֹͣ�˶������˶�ʱ��Ϊt����λ���룩��
��1����t��1ʱ��P��ʾ����������
��2�����P���B�غ�ʱ��tֵ��
��3���ڵ�P�������ɵ�A����B�ٻص���A���˶������У����P���A�ľ��루�ú�t�Ĵ���ʽ��ʾ����
��4������P��ʾ����������ԭ��ľ�����2����λ����ʱ���������������������tֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ������A��B��C���㣬��M���߶�AB���е㣬��N���߶�BC��һ�����ȷֵ㣬���AB=6��BC=12�����߶�MN�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
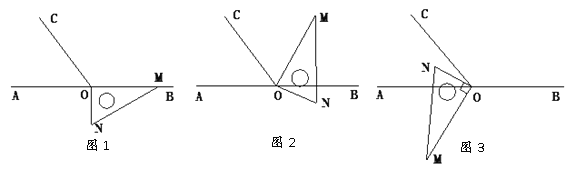
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=112��.��һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·�.
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC���ʣ�ֱ��ON�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��4����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC����t��ֵΪ���٣�
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ�����̽������AOM���NOC֮���������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���һ��քe��������Ĵ��ߣ�����������Χ�ɾ��ε��ܳ�����ֵ���������ֵ��ȣ�������������г�㣮���磮ͼ�й���P�քe��x�ᣬy��Ĵ��ߣ���������Χ�ɾ���OAPB���ܳ�����ֵ���������ֵ��ȣ����P�Ǻ�г�㣮
��1���жϵ�M��1��2����N��4��4���Ƿ�Ϊ��г�㣬��˵�����ɣ�
��2������г��P��a��3����ֱ��y=��x+b��bΪ�������ϣ���a��b��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABC�ı�BC��y����������ϣ���A��x����������ϣ���C������Ϊ��0��8��������ABC��ֱ��AB�۵�����C����x��ĸ�����D����4��0������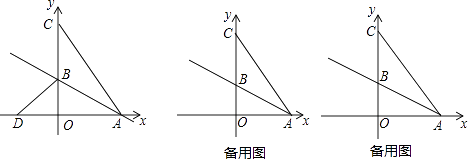
��1����ֱ��AB�Ľ���ʽ��
��2����P�ӵ�A������ÿ��4 ![]() ����λ���ȵ��ٶ�������AB�����˶�������P��PQ��AB����x���ڵ�Q��PR��AC��x���ڵ�R�����P�˶�ʱ��Ϊt���룩���߶�QR��Ϊd����d��t�ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
����λ���ȵ��ٶ�������AB�����˶�������P��PQ��AB����x���ڵ�Q��PR��AC��x���ڵ�R�����P�˶�ʱ��Ϊt���룩���߶�QR��Ϊd����d��t�ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����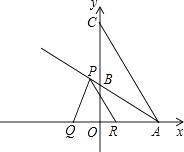
��3���ڣ�2���������£���N������AB��һ�㣬�Ե�NΪԲ�ģ�ͬʱ����R��Q��������N����N��y���ڵ�E��F���Ƿ����t��ʹ��EF=RQ�������ڣ����t��ֵ�������Բ��N�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����ѧ����ͬ��ϵ�е�У����ѡ��ͬ��ʽ��������ѧ��ѧУ��������У����ʽѡ��������˳������飬�����Ϊ��ʽA��B��C��D���֣�ÿλ����ֻ��ѡ��һ�ֿ�ʽ���ֽ�����ͳ�ƽ���Ƴ�������������������ͳ��ͼ������������ͳ��ͼ���ش��������⣺
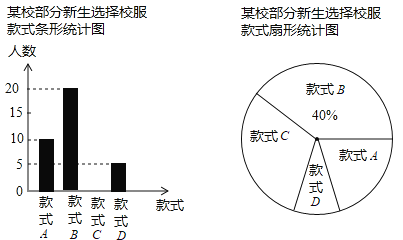
��1���ڱ��ε����У�һ����ȡ�˶���������������ȫ����ͳ��ͼ��
��2������У��847����������װ����������270��B��ʽ��У�������㰴���ͳ��֪ʶ�ж��Ƿ�Ҫ��������B��ʽ��У����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC������Բ���е�ΪD��E��F,��AD��BE�ij�Ϊ����![]() �������������ABC���ܳ�Ϊ ______��
�������������ABC���ܳ�Ϊ ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ����ڼ䣬������վ�Ӵ��˰������ȣ�ԭ���ڱ��㳡ִ�ڵ���10�ˣ����Ϲ㳡ִ�ڵ���6�ˣ��ֵ�50��ȥ֧Ԯ����������㳡x�ˣ�
��1�����Ϲ㳡��Ԯ����ִ�ڶ����ˣ��ú�x�Ĵ���ʽ��ʾ����
��2����Ҫʹ�ڱ��㳡ִ�����������Ϲ㳡ִ��������2������Ӧ�������㳡���Ϲ㳡�����������ˣ�
��3��ͨ���ʵ��ĵ���֧Ԯ������ʹ�ڱ��㳡ִ������ǡ�������Ϲ㳡ִ��������n����n�Ǵ���1����������������1���������������n��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com