
【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
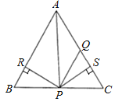
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).
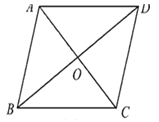
A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C﹣D﹣E上移动,若点C,D,E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )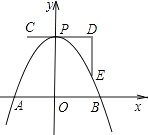
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图像与反比例函数y= ![]() (x>0)的图像交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图像交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.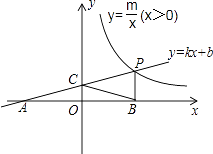
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图像上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外兴趣小组活动时,老师出示了如下问题:如图①,已知在四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=![]() AC.
AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决该问题.
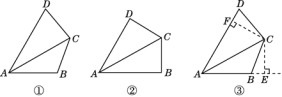
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图②,可证AB+AD=![]() AC.请你完成此证明.
AC.请你完成此证明.
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB,AD的垂线,垂足分别为点E,F,如图③.请你补全证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,后解答: ![]() =
= ![]() =
= ![]() =3+
=3+ ![]()
像上述解题过程中, ![]() ﹣
﹣ ![]() 与
与 ![]() +
+ ![]() 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)![]() 的有理化因式是;
的有理化因式是; ![]() +2的有理化因式是
+2的有理化因式是
(2)将下列式子进行分母有理化: ![]() =;
=; ![]() = .
= .
(3)已知a= ![]() ,b=2﹣
,b=2﹣ ![]() ,比较a与b的大小关系.
,比较a与b的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[动手操作] 如图所示,地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无缝隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出用一种相同的正多边形材料铺地面的方案?并画出草图.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com