
| A. | 75° | B. | 120° | C. | 90° | D. | 150° |
分析 根据已知条件R=$\frac{a\sqrt{bc}}{b+c}$,两边同乘以2得到2R=$\frac{2a\sqrt{bc}}{b+c}$=2a$•\frac{\sqrt{bc}}{b+c}$≤a,化简得到sinA≥1,于是得到sinA=1,就可得到结论.
解答 解:∵△ABC的三边长分别为a、b、c,其外接圆半径为R,
∵R=$\frac{a\sqrt{bc}}{b+c}$,
∴2R=$\frac{2a\sqrt{bc}}{b+c}$=2a$•\frac{\sqrt{bc}}{b+c}$≤a,
∵$\frac{a}{sinA}$=2R≤a,
∴sinA≥1,
∴sinA=1,
∴∠A=90°,
故选C.
点评 本题考查了三角形的外接圆与圆心,正弦定理,特殊角的三角函数,掌握正弦定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
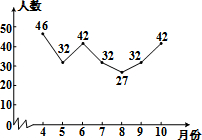 小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )| A. | 46 | B. | 42 | C. | 32 | D. | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
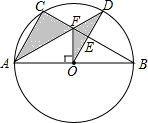 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2$\sqrt{3}$.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com