
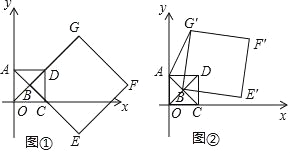
【题目】在平面直角坐标系中,O为坐标原点,点A(0,1),点C(1,0),正方形AOCD的两条对角线的交点为B,延长BD至点G,使DG=BD,延长BC至点E,使CE=BC,以BG,BE为邻边作正方形BEFG.
(Ⅰ)如图①,求OD的长及![]() 的值;
的值;
(Ⅱ)如图②,正方形AOCD固定,将正方形BEFG绕点B逆时针旋转,得正方形BE′F′G′,记旋转角为α(0°<α<360°),连接AG′.
①在旋转过程中,当∠BAG′=90°时,求α的大小;
②在旋转过程中,求AF′的长取最大值时,点F′的坐标及此时α的大小(直接写出结果即可).
【答案】(Ⅰ)![]() (Ⅱ)①α=30°或150°时,∠BAG′=90°②当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为
(Ⅱ)①α=30°或150°时,∠BAG′=90°②当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为![]() +2,此时α=315°,F′(
+2,此时α=315°,F′(![]() +
+![]() ,
,![]() ﹣
﹣![]() )
)
【解析】
(1)根据正方形的性质以及勾股定理即可解决问题,(2)①因为∠BAG′=90°,
BG′=2AB,可知sin∠AG′B=![]() ,推出∠AG′B=30°,推出旋转角α=30°,据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°,②当α=315°时,A、B、F′在一条直线上时,AF′的长最大.
,推出∠AG′B=30°,推出旋转角α=30°,据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°,②当α=315°时,A、B、F′在一条直线上时,AF′的长最大.
(Ⅰ)如图1中,
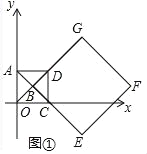
∵A(0,1),
∴OA=1,
∵四边形OADC是正方形,
∴∠OAD=90°,AD=OA=1,
∴OD=AC=![]() =
=![]() ,
,
∴AB=BC=BD=BO=![]() ,
,
∵BD=DG,
∴BG=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
(Ⅱ)①如图2中,
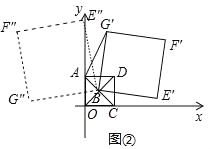
∵∠BAG′=90°,BG′=2AB,
∴sin∠AG′B=![]() =
=![]() ,
,
∴∠AG′B=30°,
∴∠ABG′=60°,
∴∠DBG′=30°,
∴旋转角α=30°,
根据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°,
综上所述,旋转角α=30°或150°时,∠BAG′=90°.
②如图3中,连接OF,
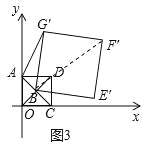
∵四边形BE′F′G′是正方形的边长为![]()
∴BF′=2,
∴当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为![]() +2,
+2,
此时α=315°,F′(![]() +
+![]() ,
,![]() ﹣
﹣![]() )
)


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,设一次函数![]() 的图象是直线
的图象是直线![]() .
.
(1)如果把![]() 向下平移
向下平移![]() 个单位后得到直线
个单位后得到直线![]() ,求
,求![]() 的值;
的值;
(2)当直线![]() 过点
过点![]() 和点
和点![]() 时,且
时,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若坐标平面内有点![]() ,不论
,不论![]() 取何值,点
取何值,点![]() 均不在直线
均不在直线![]() 上,求
上,求![]() 所需满足的条件.
所需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员推铅球,铅球运行时离地面的高度![]() (米)是关于运行时间
(米)是关于运行时间![]() (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为![]() 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
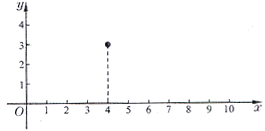
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=a ,AB=c,AC=b,则不能作为判定△ABC是直角三角形的条件的是( )
A.![]() B.∠A∶∠B∶∠C=1∶4∶3
B.∠A∶∠B∶∠C=1∶4∶3
C.a∶b∶c =7∶24∶25D.a∶b∶c =4∶5∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似地,可以在等腰三角形中建立边角之间的关系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad)如图1,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad![]() .容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解答下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解答下列问题:
(1)sad![]() = ;
= ;
(2)对于![]() <A<
<A<![]() ,∠A的正对值sadA的取值范围 ;
,∠A的正对值sadA的取值范围 ;
(3如图2,已知sinA=![]() ,其中∠A为锐角,试求sadA的值。
,其中∠A为锐角,试求sadA的值。


查看答案和解析>>
科目:初中数学 来源: 题型:
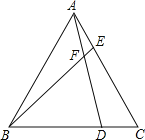
【题目】 如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD = AE,AD与BE相交于点F.
(1)求证:AD = BE;
(2)求∠BFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
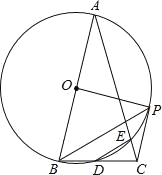
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com