先化简.再求值÷(2a-$\frac{{a}^{2}-2a-1}{a-2}$).其中a=4cos60°+1．题目和参考答案——青夏教育精英家教网—

10．先化简，再求值（1+$\frac{1}{a-2}$）÷（2a-$\frac{{a}^{2}-2a-1}{a-2}$），其中a=4cos60°+1．

分析直接利用分式混合运算法则化简，进而把已知化简代入求出答案．

解答解：原式=$\frac{a-1}{a-2}$÷$\frac{2{a}^{2}-4a-{a}^{2}+2a+1}{a-2}$
=$\frac{1}{a-1}$，
当a=4cos60°+1=3时，
原式=$\frac{1}{a-1}$=$\frac{1}{2}$．

点评此题主要考查了分式的化简求值以及特殊角的三角函数值，正确进行分式的混合运算是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

20．以△ABC的边AB，AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，M为EG的中点，连接AM．
（1）如图1，∠BAC=90°，试判断AM与BC关系？
（2）如图2，∠BAC≠90°，图1中的结论是否成立？若不成立，说明理由；若成立，给出证明．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．下列调查中，适宜采用普查方式的是（　　）

	A．	国家旅游局调查国民对“五一”期间出行旅游的满意程度
	B．	调查中国民众对美国在韩部署萨德系统持反对态度的比例
	C．	调查中国国产航母各零部件的质量
	D．	调查重庆市初2017级学生的中考体考成绩

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．解不等式组：$\left\{\begin{array}{l}{3-（2x-1）≥5x+4}\\{\frac{x}{2}-3＜2x}\end{array}\right.$，并把解集在数轴上表示出来．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发匀速前行，且途中休息一段时间后继续以原速前行．家到公园的距离为2000m，如图是小明和爸爸所走的路程S（m）与步行时间t（min）的函数图象．
（1）直接写出BC段图象所对应的函数关系式（不用写出t的取值范围）．
（2）小明出发多少时间与爸爸第三次相遇？
（3）在速度都不变的情况下，小明希望比爸爸早18分钟到达公园，则小明在步行过程中停留的时间需减少3分钟．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

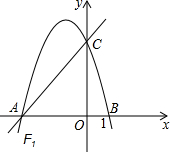如图，直线y=$\frac{4}{3}$x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F₁交x轴于另一点B（1，0）．
（1）求抛物线F₁所表示的二次函数的表达式及顶点Q的坐标；
（2）在抛物线上是否存在点P，使△BPC的内心在y轴上，若存在，求出点P的坐标，若不存在写出理由；
（3）直线y=kx-6与y轴交于点N，与直线AC的交点为M，当△MNC与△AOC相似时，求点M坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．（1）计算：$\root{3}{27}$+|$\sqrt{5}$-2|-（$\frac{1}{3}$）^-2+（tan60°-1）⁰
（2）先化简再求值：（$\frac{{{a^2}-5a+2}}{a+2}$+1）÷$\frac{{{a^2}-4}}{{{a^2}+4a+4}}$，其中a=2+$\sqrt{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

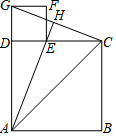如图，已知四边形ABCD和四边形DEFG为正方形，点E在线段DC上，点A、D、G在同一直线上，且AD=3，DE=1，连接AC、CG、AE，并延长AE交OG于点H．
（1）求证：∠DAE=∠DCG．
（2）求线段HE的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．先化简，再求值：$\frac{1}{x-y}$÷（$\frac{1}{y}$-$\frac{1}{x}$），其中x=$\sqrt{3}$+$\sqrt{2}$，y=$\sqrt{3}$-$\sqrt{2}$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学