
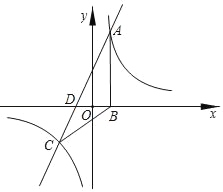
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、C两点,与x轴交于点D,过点A作AB⊥x轴于点B,点O是线BD的中点,AD=2
(k≠0)的图象交于A、C两点,与x轴交于点D,过点A作AB⊥x轴于点B,点O是线BD的中点,AD=2![]() ,cos∠ADB=
,cos∠ADB=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当x为何值时,y1≥y2.
【答案】(1)y2=![]() ,一次函数解析式为y1=2x+2;(2)当﹣2≤x<0或x≥1时,y1≥y2.
,一次函数解析式为y1=2x+2;(2)当﹣2≤x<0或x≥1时,y1≥y2.
【解析】
(1)先解Rt△ABD,根据余弦函数的概念求出BD,根据勾股定理求出AB,再利用待定系数法求出反比例函数和一次函数的解析式;
(2)先联立反比例函数和一次函数的解析式,得到方程组,求出C点坐标,再观察图象,得到y1≥y2时x的取值范围.
解:(1)∵在Rt△ABD中,∠ABD=90°,AD=2![]() ,cos∠ADB=
,cos∠ADB=![]() ,
,
∴BD=ADcos∠ADB=2![]() ×
×![]() =2,
=2,
由勾股定理得,AB=![]() =
=![]() =4,
=4,
∵点O是线段BD的中点,
∴点A的坐标为(1,4),点D的坐标为(﹣1,0).
把A(1,4)代入y2=![]() ,得反比例函数的解析式为:y2=
,得反比例函数的解析式为:y2=![]() .
.
把A(1,4),D(﹣1,0)代入y1=ax+b,
得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y1=2x+2;
(2)由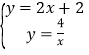 ,解得
,解得![]() ,或
,或![]() ,
,
∴C(﹣2,﹣2).
由图象可知,当﹣2≤x<0或x≥1时,一次函数y1=ax+b(a≠0)的图象在反比例函数y2=![]() (k≠0)图象的上方,
(k≠0)图象的上方,
∴当﹣2≤x<0或x≥1时,y1≥y2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
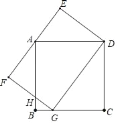
【题目】如图,点G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
(1)寻找并证明图中的两组相似三角形;
(2)求HG、FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
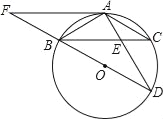
【题目】如图,△ABC为圆O的内接三角形,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
(1)求证:△ABE∽△ADB,并求AB的长;
(2)延长DB到F,使BF=BO,连接FA,那么直线FA与⊙O相切吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,兰博基尼某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,车门打开是绕点A逆时针旋转至CD与AD垂直,已知四边形ABCD与四边形AB′C′D′在同一平面,若AD∥BC,∠D=45°,∠DAB′=30°,CD=60cm,则AB的长约为( )(![]() ≈1.7)
≈1.7)
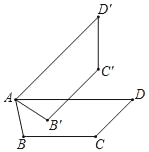
A. 21cmB. 42cmC. 51cmD. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
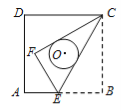
A.4![]() B.
B. ![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com