
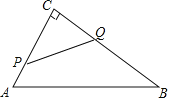
【题目】如图,在![]() 中,
中,![]() ,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(
,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(![]() )与运动时间x(s)之间的函数图象为( )
)与运动时间x(s)之间的函数图象为( )
A. 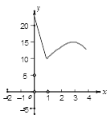 B.
B. 
C. 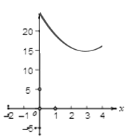 D.
D. 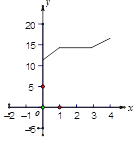
科目:初中数学 来源: 题型:
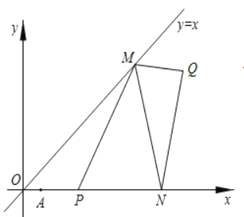
【题目】平面直角坐标系中,直线![]() ,点
,点![]() ,点
,点![]() ,动点
,动点![]() 在直线
在直线![]() 上,动点
上,动点![]() 、
、![]() 在
在![]() 轴正半轴上,连接
轴正半轴上,连接![]() 、
、![]() 、
、![]() .
.
(1)若点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(2)如图![]() ,当
,当![]() 周长最小时,连接
周长最小时,连接![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
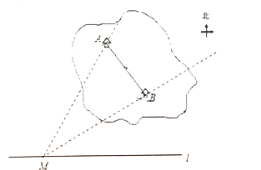
【题目】小强想知道湖中两个小亭A、B之间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道I上某一观测点M处,测得亭A在点M的北偏东30°,亭B在点M的北偏东60°,当小明由点M沿小道I向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小强计算湖中两个小亭A、B之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.
(1)求k的值;
(2)设抛物线与直线y=﹣![]() (x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,
(x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,![]() )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
)两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
(3)将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的是某超市入口的双翼闸门,如图2,当它的双翼展开时,双翼边缘的端点A与B 之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,联接PA,若AB=4,∠BAD=60°,则PA的最小值是( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() ﹣2 D. 4
﹣2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
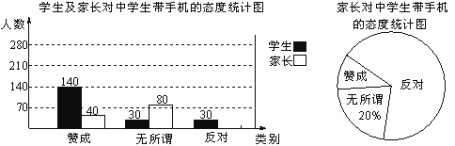
【题目】“校园手机”现象越来越受到社会的关注,小记者张明随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如图所示的统计图:
(1)这次调查的总人数有_____人;
(2)补全两个统计图;
(3)针对随机调查的情况,张明决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小明的家长,小亮和小明的家长被同时选中的概率是_____.(以上三个问题均不需写过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com