练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．作函数y=|2x-1|+|x+1|的图象．

    分析 根据题意，结合绝对值的意义，可得y=|2x-1|+|x+1|=$\left\{\begin{array}{l}{-3x（x＜-1）}\\{-x+2（-1≤x≤\frac{1}{2}）}\\{3x（x＞\frac{1}{2}）}\end{array}\right.$，进而分段做出图象即可．

    解答 解：根据题意，结合绝对值的意义，
    可得y=|2x-1|+|x+1|=$\left\{\begin{array}{l}{-3x（x＜-1）}\\{-x+2（-1≤x≤\frac{1}{2}）}\\{3x（x＞\frac{1}{2}）}\end{array}\right.$，
    进而分段作出图象可得．

    点评 本题考查一次函数图象的变化及分段函数图象的作法，注意绝对值的化简方法即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．如图，∠1=40°，如果CD∥BE，那么∠B的度数为140°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，已知GH∥EF，不能使AB∥CD的是（　　）
    A．∠1=∠4B．∠1=∠2，∠3=∠4C．∠2=∠4D．∠1+∠2=∠5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．（1）点M（3，0）到点N（-2，0）的距离是$\sqrt{13}$．
    （2）点C在y轴上，到坐标原点的距离为5个单位长度，则C点的坐标为（0，5）或（0，-5）．
    （3）点D在y轴左侧，它到x轴距离为2个单位长度，到y轴距离为1个单位长度，则D点坐标为（-1，2）或（-1，-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．若a的两个平方根为x、y，且满足方程3x+2y=2．
    （1）求a的值；
    （2）求a2的算术平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知∠ABC=90°，D是直线AB上的点，AD=BC．
    （1）如图1，过点A作AF⊥AB，并截取AF=BD，连接DC，DF，CF，判断△CDF的形状并证明；
    （2）如图2，E是直线BC上的一点，直线AE，CD相交于点P，且∠APD=45°，求证：BD=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在△ABC中，AD为BC边上的中线，
    （1）如图1，求证：AB+AC＞2AD；
    （2）如图2，若∠BAC＜90°，作EA⊥AC，FA⊥BA，且AE=AC，AF=AB，连接EF，写出AD与EF的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

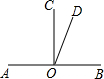    4．如图，直线AB过点O，OC、OD是直线AB同旁的两条射线，若∠BOD比∠COD的3倍还大20°，∠AOD比∠BOD的2倍小15°．求∠COD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．下列问题哪些是必然事件？哪些是不可能事件？哪些是随机事件？
    （1）太阳从西边落山；
    （2）某人的体温是100℃；
    （3）a2+b2=-1（其中a、b都是实数）；
    （4）水往低处流；
    （5）经过有信号灯的十字路口，遇见红灯．

    查看答案和解析>>

    同步练习册答案