
���� ��1������ͼ��ȷ����Pλ�ü��ɽ�����⣮
��2�����������ٵ�P��OB�ϣ��ڵ�P��OD��ʱ���OP���ɽ�����⣮
��3��������������ͼ4�У�����P��OB��ʱ������ͼ5�У�����P��OD��ʱ��CM��·�������������ʼ6s��·������3s��·�����ɽ�����⣮
��4����ABQ��������䣬����������֤�����ɢٵ���P��OB��ʱ����ͼ6�У���QH��BD��H������S��ABQ=S��ABP+S��QBP+S��APQ���㼴�ɣ�
�ڵ���P��OD��ʱ����ͼ7�У���QH��BD��H������S��ABQ=S��ABP+S��APQ-S��QBP���㼴�ɣ�
��� �⣺��1����ͼ1�У�AC��BD���ڵ�O��
�ߡ�DAB=��ABC=90�㣬DA=AB=BC=6$\sqrt{2}$cm��
�ߡ�BAC=��ABD=45�㣬
��OA=OB=OD=6��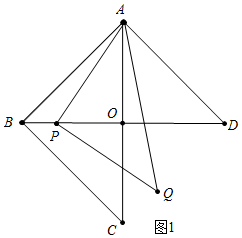
��Q��C�غ�ʱ����P��B�غϣ���ʱt=0��
����Q��D�غ�ʱ����P��O�غϣ���ʱt=6��
�ʴ�Ϊ0s��6s��
��2������ͼ2�У�����P��OB��ʱ��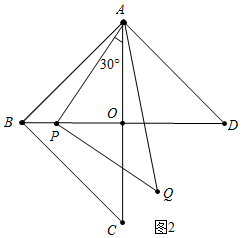
�ߡ�PAO=30�㣬��AOP=90�㣬OA=6��
��PO=OA•tan30��=2$\sqrt{3}$��
��PB=6-2$\sqrt{3}$��
��t=6-2$\sqrt{3}$
����ͼ3�У���P��OD��ʱ��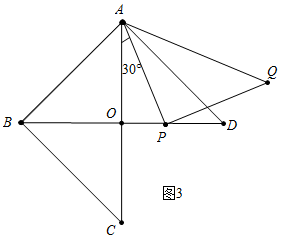
��֪OP=2$\sqrt{3}$��BP=6+2$\sqrt{3}$����ʱt=6+2$\sqrt{3}$��
����������t=��6-2$\sqrt{3}$��s��6+2$\sqrt{3}$��sʱ����PAC=30�㣮
��3������ͼ4�У�����P��OB��ʱ��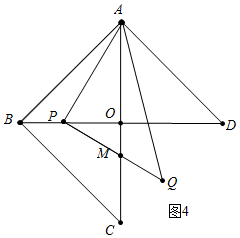
�ߡ�AOP�ס�APM��
��$\frac{AP}{AM}$=$\frac{OA}{AP}$��
��AP2=OA•AM��
�ࣨ6-t��2+62=6��12-y����
��y=-$\frac{1}{6}$t2+2t��
����ͼ5�У�����P��OD��ʱ��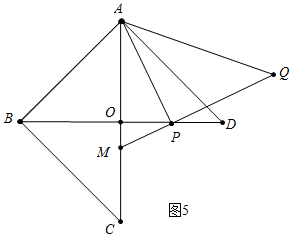
ͬ����PA2=AO•AM��
��62+��t-6��2=6��12-y����
��y=-$\frac{1}{6}$t2+2t��
����������y=-$\frac{1}{6}$t2+2t����0��t��12����
��y=-$\frac{1}{6}$��t-6��2+6��
��t=6ʱ��y�����ֵΪ6��
�֡�t=9ʱ��y=4.5��
���ʱOM=1.5��
��0��t��9ʱ��CM�˶���·��Ϊ6+1.5=7.5cm��
��4�����ۣ�S��ABQ��ֵ���䣮�������£�
�ٵ���P��OB��ʱ����ͼ6�У���QH��BD��H��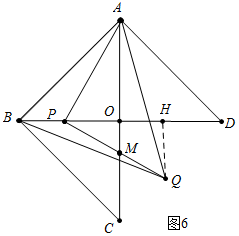
��AP=PQ����APO=��PQH����AOP=��PHQ��
���APO�ա�PQH��
��QH=OP=6-t��
��S��ABQ=S��ABP+S��QBP+S��APQ=$\frac{1}{2}$•t•6+$\frac{1}{2}$•t•��6-t��+$\frac{1}{2}$[62+��6-t��2]=36��
�ڵ���P��OD��ʱ����ͼ7�У���QH��BD��H��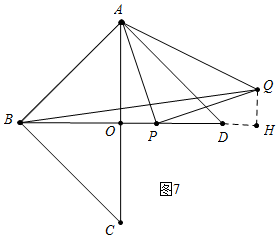
ͬ����֤QH=OP=t-6��
S��ABQ=S��ABP+S��APQ-S��QBP=$\frac{1}{2}$•t•6+$\frac{1}{2}$•t•��t-6��-$\frac{1}{2}$[62+��t-6��2]=36��
���ABQ�����Ϊ��ֵ��
���� ���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ����������ε������֪ʶ������Ĺؼ���ѧ��������۵�˼��˼�����⣬ѧ���÷ָ�������ε�����������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
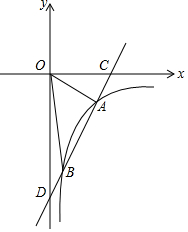 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0���뷴��������y=$\frac{k}{x}$��k��0��x��0������A��B���㣬��x�ᡢy��ֱ���C��D���㣬����OA��OB����OA=2$\sqrt{13}$��sin��AOC=$\frac{2\sqrt{13}}{13}$����B������Ϊ��m��-8��
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0���뷴��������y=$\frac{k}{x}$��k��0��x��0������A��B���㣬��x�ᡢy��ֱ���C��D���㣬����OA��OB����OA=2$\sqrt{13}$��sin��AOC=$\frac{2\sqrt{13}}{13}$����B������Ϊ��m��-8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��D��E�ֱ��ǡ�ABC����AB��AC�ϵĵ㣬���������������¡�ADE���ACB�Ƿ����ƣ���˵�����ɣ�
��֪����ͼ��D��E�ֱ��ǡ�ABC����AB��AC�ϵĵ㣬���������������¡�ADE���ACB�Ƿ����ƣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
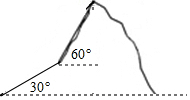 ��ͼ��ij������30���ɽ��ǰ��1000m����ɽ��������Ϊ60�㣬��ǰ��1500m�������ɽ����������ɽ�ĸ߶ȣ�������������
��ͼ��ij������30���ɽ��ǰ��1000m����ɽ��������Ϊ60�㣬��ǰ��1500m�������ɽ����������ɽ�ĸ߶ȣ��������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
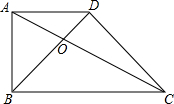 ��ͼ�����ı���ABCD�У�AD��BC���Խ���AC��BD�ཻ�ڵ�O��AD=BC=4�����AOD���BOC������ȣ�
��ͼ�����ı���ABCD�У�AD��BC���Խ���AC��BD�ཻ�ڵ�O��AD=BC=4�����AOD���BOC������ȣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com