
【题目】某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
![]()
A.A区B.B区C.C区D.A.B两区之间
【答案】A
【解析】
根据题意分别计算停靠点分别在A、B、C各点和A区、B区之间时员工步行的路程和,选择最小的即可求解.
解:∵当停靠点在A区时,所有员工步行到停靠点路程和是:
15×100+10×300=4500m,
当停靠点在B区时,所有员工步行到停靠点路程和是:30×100+10×200=5000m,
当停靠点在C区时,所有员工步行到停靠点路程和是:30×300+15×200=12000m,
当停靠点在A、B区之间时,
设在A区、B区之间时,设距离A区x米,
则所有员工步行路程之和=30x+15(100-x)+10(100+200-x),
=30x+1500-15x+3000-10x,
=5x+4500,
∴当x=0时,即在A区时,路程之和最小,为4500米;
综上,当停靠点在A区时,所有员工步行到停靠点路程和最小,那么停靠点的位置应该在A区.
故选:A.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
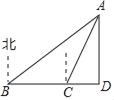
【题目】如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向上,轮船从B处继续向正东方向航行100海里到达C处时,测得小岛A在船的北偏东30°的方向上,AD⊥BC于点D,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
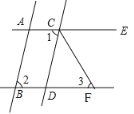
(1)试判断直线AE与BF有怎样的位置关系,并说明理由;
(2)若∠1=80°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+ ![]() 经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.
经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.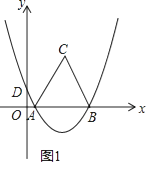
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM= ![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长.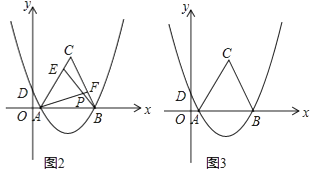
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是A,B,C,D三点,按如下步骤作图:①先分别以A,B两点为圆心,以大于 ![]() AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于
AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于 ![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )
的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )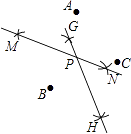
A.100°
B.120°
C.132°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了搞好对“传统文化学习”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题: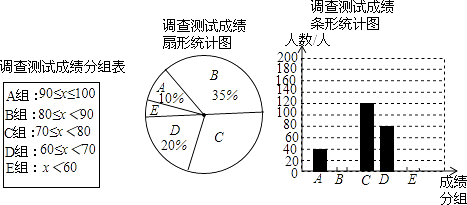
(1)参加调查测试的学生为人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
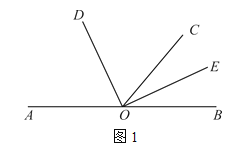
【题目】已知,O为直线AB上一点,∠DOE=90°.
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
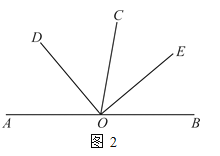
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.

(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com