
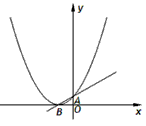
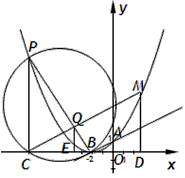
| 解:(1)当a=0时,y=x+1,图象与x轴只有一个公共点, 当a≠0时,△=1-4a=0,a= 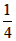 ,此时,图象与x轴只有一个公共点, ,此时,图象与x轴只有一个公共点,∴函数的解析式为:y=x+1或y= 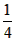 x2+x+1; x2+x+1;(2)设P为二次函数图象上的一点,过点P作PC⊥x 轴于点C, ∵y=ax2+x+1是二次函数,由(1)知该函数关系式为:y= 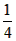 x2+x+1,则顶点为B(-2,0), x2+x+1,则顶点为B(-2,0),图象与y轴的交点坐标为A(0,1), ∵以PB为直径的圆与直线AB相切于点B, ∴PB⊥AB,则∠PBC=∠BAO, ∴Rt△PCB∽Rt△BOA, ∴ 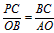 ,故PC=2BC, ,故PC=2BC,设P点的坐标为(x,y), ∵∠ABO是锐角,∠PBA是直角, ∴∠PBO是钝角, ∴x<-2, ∴BC=-2-x,PC=-4-2x,即y=-4-2x,P点的坐标为(x,-4-2x), ∵点P在二次函数y= 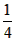 x2+x+1的图象上, x2+x+1的图象上,∴-4-2x= 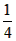 x2+x+1, x2+x+1,解之得:x1=-2,x2=-10, ∵x<-2, ∴x=-10, ∴P点的坐标为:(-10,16); (3)点M不在抛物线y=ax2+x+1上, 由(2)知:C为圆与x轴的另一交点,连接CM, CM与直线PB的交点为Q,过点M作x轴的垂线,垂足为D, 取CD的中点E,连接QE,则CM⊥PB,且CQ=MQ, ∴QE∥MD,QE= 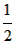 MD,QE⊥CE, MD,QE⊥CE,∵CM⊥PB,QE⊥CE,PC⊥x轴, ∴∠QCE=∠EQB=∠CPB, ∴tan∠QCE=tan∠EQB=tan∠CPB= 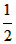 , ,CE=2QE=2×2BE=4BE, 又CB=8,故BE= 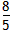 ,QE= ,QE=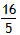 , ,∴Q点的坐标为(- 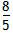 , ,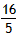 ), ),可求得M点的坐标为 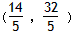 , ,∵ 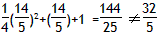 , ,∴C点关于直线PB的对称点M不在抛物线y=ax2+x+1上。 |
 |


科目:初中数学 来源: 题型:
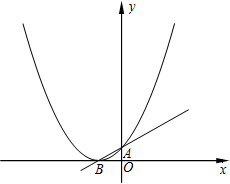 已知:函数y=ax2+x+1的图象与x轴只有一个公共点.
已知:函数y=ax2+x+1的图象与x轴只有一个公共点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
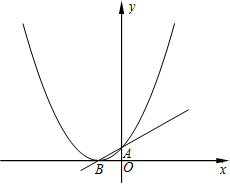 已知:函数y=ax2+x+1的图象与x轴只有一个公共点.
已知:函数y=ax2+x+1的图象与x轴只有一个公共点.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(30):2.8 二次函数的应用(解析版) 题型:解答题
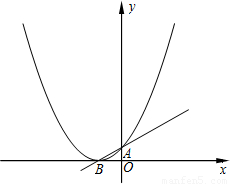
查看答案和解析>>
科目:初中数学 来源:2012年江苏省盐城市响水县中考数学二模试卷(解析版) 题型:解答题
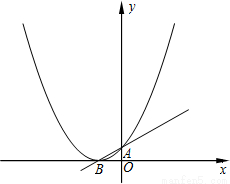
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com