
分析 (1)分别根据数的乘方法则及开方法则、特殊角的三角函数值及绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=1-3$\sqrt{2}$+2×$\frac{\sqrt{2}}{2}$-2
=1-3$\sqrt{2}$+$\sqrt{2}$-2
=-1-2$\sqrt{2}$;
(2)原式=$\frac{x+1-x+1}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2}{x}$,
当x=2时,原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
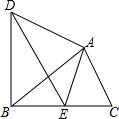 如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.
如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
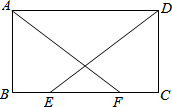 如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四条边都相等的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 对角线互相垂直平分且相等的四边形是正方形 | |
| D. | 一组对边平行,另一组对边相等的四边形是等腰梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com