练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在一个直角坐标系中，描出下列各点：

    A(－1，0)，B(3，0)，C(4，2)，D(0，2)

    (1)把点A，B，C，D，A顺次连结成封闭图形．你会得到什么形状的图形？

    (2)如果各顶点的横坐标都加1，纵坐标不变，将新得到的顶点依次连结成封闭图形，那么新的图形与(1)中图形的位置有怎样的关系？形状呢？

    (3)如果各顶点的横坐标不变，纵坐标都加1，将新得到的顶点依次连结成封闭图形，那么新的图形与(1)中图形的位置有怎样的关系？形状呢？

    (4)如果各顶点的横坐标变为它的相反数，纵坐标不变，将新得到的顶点依次连结成封闭图形，那么新的图形与(1)中图形的位置有怎样的关系？形状呢？

    (5)如果各顶点的横坐标不变，纵坐标变为它的相反数，将新得到的顶点依次连结成封闭图形，那么新的图形与(1)中图形的位置有怎样的关系？形状呢？

    (6)如果各顶点的横坐标、纵坐标都变为它的相反数，将新得到的顶点依次连结成封闭图形，那么新的图形与(1)中图形的位置有怎样的关系？形状呢？

    答案：略
    解析：

    (1)得到的图形是平行四边形；

    (2)对应的新顶点是坐标分别为，新图形是原图形向右平移了1个单位长度，形状不变；

    (3)对应的新顶点的坐标分别为，新图形是原图形向上平移了1个单位长度，形状不变；

    (4)对应的新顶点的坐标分别为，新图形与原图形关于y轴对称，形状不变；

    (5)对应的新顶点的坐标分别为，新图形与原图形关于x轴对称，形状不变；

    (6)对应的新顶点的坐标分别为，新图形与原图形关于原点对称，形状不变．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某文具店出售书包和文具盒，书包每个定价30元，文具盒每个定价5元，该店制定两种优惠方案：①买一个书包赠送一个文具盒；②按总价九折付款．若某班需购8个书包，文具盒若干个（不少于8个），如果设购文具盒数为x（个），付款为y（元）
    （1）分别求出两种优惠方案中y与x之间的函数关系式；
    （2）在同一直角坐标系中画出这两个函数的图象；
    （3）根据图象回答，购买多少个文具盒时，两种方案用钱相同；
    （4）若购买60个文具盒时，两种方案哪一种最省钱．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    15、一个平行四边形在平面直角坐标系中三个顶点的坐标分别是（-1，-1），（-2，3），（3，-1），则第四个顶点的坐标为
    （2，3）或（-6，3）或（4，-5）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标精英家教网为（0，8），点C的坐标为（10，0），OB=OC，
    （1）求点B的坐标；
    （2）点P从C点出发，沿线段CO以1个单位/秒的速度向终点O匀速运动，过点P作PH⊥OC，交折线C-B-O于点H，设点P的运动时间为t秒（0≤t≤10），
    ①是否存在某个时刻，使△OPH的面积等于△OBC面积的
    320
    ？若存在，求出t的值；若不存在，请说明理由；
    ②以P为圆心，PC长为半径作⊙P，当⊙P与线段OB只有一个公共点时，求t的值或t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

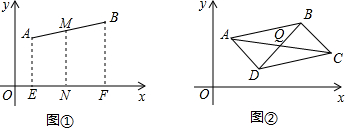    让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
    第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是
    1
    1
    ． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
    第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x1，y1），B（x2，y2），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（
    x1+x2
    2
    x1+x2
    2
    ，
    y1+y2
    2
    y1+y2
    2
     ）（用x1，y1，x2，y2表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
    第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则其对角线交点Q的坐标可以表示为Q（
    x1+x3
    2
    x1+x3
    2
    ，
    y1+y3
    2
    y1+y3
    2
    ），也可以表示为Q（
    x2+x4
    2
    x2+x4
    2
    ，
    y2+y4
    2
    y2+y4
    2
     ），经过比较，我们可以分别得出关于x1，x2，x3，x4及，y1，y2，y3，y4的两个等式是
    x1+x3=x2+x4
    x1+x3=x2+x4
    和
    y1+y3=y2+y4
    y1+y3=y2+y4
    ． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的
    和相等
    和相等
    ．

    查看答案和解析>>

    同步练习册答案