
【题目】已知![]() ,点
,点![]() 为射线
为射线![]() 上一点,点
上一点,点![]() 为
为![]() 的中点,且
的中点,且![]() .当点
.当点![]() 在射线
在射线![]() 上运动时 ,则
上运动时 ,则![]() 与
与![]() 和的最小值为_______.
和的最小值为_______.
【答案】![]()
【解析】
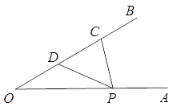
作点D关于OA的对称点D′,连接CD′交OA于点P′,连接DP,,根据轴对称的性质得到P′D′=P′D,此时DP′+CP′=CD′即为PC+PD的最小值,根据已知条件计算求出结果即可.
解:作点D关于OA的对称点D′,连接CD′交OA于点P′,连接DP′,根据轴对称的性质得到P′D′=P′D,此时DP′+CP′=CD′即为PC+PD的最小值.
设DD′与OA交于点E,
∵∠O=30°,OD=3,由对称性可知∠DEO=90°,
∴∠ODE=60°,DE=![]() OD=
OD=![]() ,
,
∴DD′=2DE=3,∴DD′=CD,
∴∠D′=∠DCD′=![]() ∠ODE=30°,∴∠EDP′=∠D′=30°,
∠ODE=30°,∴∠EDP′=∠D′=30°,
∴∠ODP′=∠ODE+∠EDP′=90°,
∴在Rt△ODP′中,∠O=30°,OD=3,∴DP′=![]()
∴CP′=2DP′=2![]()
∴DP′+CP′=3![]()
故![]() 与
与![]() 和的最小值为3
和的最小值为3![]()



科目:初中数学 来源: 题型:
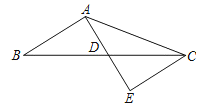
【题目】如图,在△ABC中,AB=3,AC=5,AD是BC边上的中线,且AD=2,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”. 例如:等腰直角三角形就是“半角三角形”.在钝角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 边于点
边于点![]() .点
.点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(1)若![]() ,点
,点![]() 在
在![]() 延长线上.
延长线上.
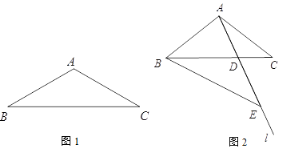
① 当![]() ,点
,点![]() 恰好为
恰好为![]() 中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
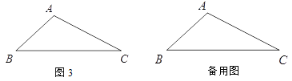
② 如图2,若![]() ,图中是否存在“半角三角形”(△
,图中是否存在“半角三角形”(△![]() 除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
(2)如图3,若![]() ,保持
,保持![]() 的度数与(1)中②的结论相同,请直接写出
的度数与(1)中②的结论相同,请直接写出![]() ,
,![]() ,
,![]() 满足的数量关系:______.
满足的数量关系:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
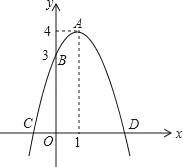
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com