
【题目】已知:如图,⊙O1和⊙O2相交于A、B两点, ⊙O1经过点O2,点C在![]() 上运动(点C 不与A、B重合),AC的延长线交⊙O2于P,连结AB、BC、BP;
上运动(点C 不与A、B重合),AC的延长线交⊙O2于P,连结AB、BC、BP;
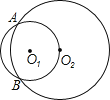
(1)按题意将图形补充完整;
(2)当点C在![]() 上运动时,图中不变的角有 (将符合要求的角都写上)
上运动时,图中不变的角有 (将符合要求的角都写上)
(3)线段BC、PC的长度存在何种关系?写出结论,并加以证明;
(4)设⊙O1和⊙O2的半径为![]() 、
、![]() ,当
,当![]() ,
,![]() 满足什么条件时,
满足什么条件时,![]() 为等腰直角三角形?
为等腰直角三角形?
【答案】(1)见解析;(2)∠ACB,∠BCP,∠APB,∠CBP;(3)CB = CP;理由见解析;(4)![]()
【解析】
(1)根据题意作图即可;
(2)由圆周角定理得∠ACB和∠APB不变,然后根据邻补角的性质和三角形外角的性质可得∠BCP和∠CBP不变;
(3)连结AO2,BO2,根据圆周角定理和三角形外角的性质求出∠CBP =∠P即可得BC = PC;
(4)由△BCP为等腰直角三角形得出弦AB为⊙O1的直径,△AO2B为等腰直角三角形,然后根据勾股定理列式计算即可.
解:(1)如图所示:
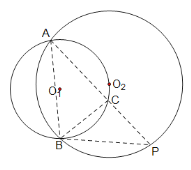
(2)由圆周角定理得:∠ACB和∠APB不变,
∴∠BCP不变,
∵∠ACB=∠APB+∠CBP,
∴∠CBP不变,
故图中不变的角有∠ACB,∠BCP,∠APB,∠CBP;
(3)BC = PC;
证明:连结AO2,BO2,
∵∠AO2B =∠ACB = 2∠P,∠ACB = ∠CBP +∠P,
∴∠CBP =∠P,
∴BC = PC;
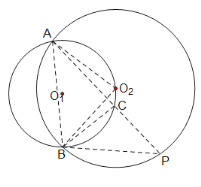
(4)要使△BCP为等腰直角三角形,已有BC=PC,只需∠BCP =90°,
∴∠ACB=90°,
∴弦AB为⊙O1的直径,
∴△AO2B为等腰直角三角形,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
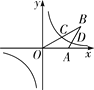
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
(k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
A.2![]() B.3
B.3![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,分别过点![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和
和![]() ,探究直线
,探究直线![]() 和
和![]() 与双曲线
与双曲线 ![]() 的关系,下列结论中错误的是
的关系,下列结论中错误的是
A.两直线中总有一条与双曲线相交
B.当![]() =1时,两条直线与双曲线的交点到原点的距离相等
=1时,两条直线与双曲线的交点到原点的距离相等
C.当![]() 时,两条直线与双曲线的交点在
时,两条直线与双曲线的交点在![]() 轴两侧
轴两侧
D.当两直线与双曲线都有交点时,这两交点的最短距离是2
查看答案和解析>>
科目:初中数学 来源: 题型:
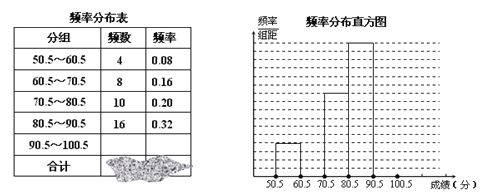
【题目】为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答: .
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答: .
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
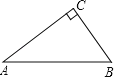
(1)以AB边上一点O为圆心作⊙O,使⊙O经过点A,C;(保留作图痕迹,不写作法)
(2)判断点B与⊙O的位置关系是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的![]() 名领操员进行比赛,成绩如下表:
名领操员进行比赛,成绩如下表:
成绩(分) |
|
|
|
|
人数(人) |
|
|
|
|
(1)这组数据的众数是______,中位数是_______;
(2)已知获得![]() 分的选手中,七、八、九年级分别有
分的选手中,七、八、九年级分别有![]() 人、
人、![]() 人、
人、![]() 人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣x+3交x轴于点B,交y轴于点A,过点A作AC⊥AB交x轴于点C.
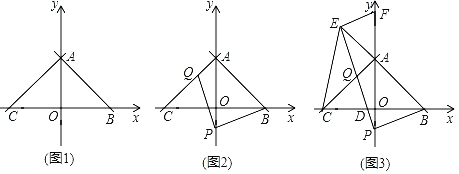
(1)如图1,求直线AC的解析式;
(2)如图2,点P在AO的延长线上,点Q在AC上,连接PB,PQ,且PQ=PB,设点P的纵坐标为t,AQ的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,PQ交x轴于点D,延长PQ交BA的延长线于点E,过点E作EF⊥PE交y轴于点F,若DE=![]() EF,求点Q的坐标.
EF,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com