练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知分式$\frac{x-4}{x（x+1）}$=0，则x的值为（　　）
    A．0B．-1C．0或-1D．4

    分析 分式的值是0的条件是：分子为0，分母不为0．

    解答 解：∵x-4=0，
    ∴x=4，
    当x=4，时x（x+1）≠0，
    ∴当x=4时，分式的值是0．
    故选D．

    点评 本题主要考查分式是0的条件，特别需要注意的是分母不能是0，这是经常考查的知识点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．如图，若AB∥CD，∠B=120°，∠C=25°，则∠α的度数为（　　）
    A．35°B．50°C．65°D．85°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

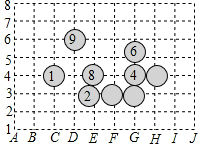    3．如图，围棋盘的左下角呈现的是2015年3月7日韩国新人王战决赛第一局中的几手棋，为记录棋谱方便，横线用数字表示，竖线用英文字母表示，这样，黑棋①的位置可记为（C，4），白棋②的位置可记为（E，3），则黑棋⑨的位置应记为（D，6）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．小明在学习二次根式时，发现一些含根号的式子可以化成另一式子的平方．如：
    5+2$\sqrt{6}$=（2+3）+2$\sqrt{2×3}$=（$\sqrt{2}$）2+（$\sqrt{3}$）2+2$\sqrt{2}$×$\sqrt{3}$=（$\sqrt{2}$$+\sqrt{3}$）2；
    8-2$\sqrt{15}$=（5+3）-2$\sqrt{5×3}$=（$\sqrt{5}$）2=（$\sqrt{3}$）2-2$\sqrt{5}$×$\sqrt{3}$=（$\sqrt{5}$$-\sqrt{3}$）2．
    （1）请你仿照小明的方法将7+2$\sqrt{10}$化成一个式子的平方；
    （2）将下列的等式补充完整：a+b-2$\sqrt{ab}$=（$\sqrt{a}$-$\sqrt{b}$）2（a≥0，b≥0），并证明这个等式；
    （3）若a+2$\sqrt{18}$=（$\sqrt{m}$$+\sqrt{n}$）2，且a、m、n均为正整数，则a=19或11或9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．求不等式$\frac{2x-1}{3}$-$\frac{5x+1}{2}$≥1的非负整数解，并在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，∠BAC=90°，∠1=∠2，AM⊥BC，AD⊥BE，那么∠2=∠3=∠4，你知道这是为什么吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．构造一个不等式组，其解集是-1＜x≤2，则你构造的一元一次不等式组是$\left\{\begin{array}{l}{x+1＞0}\\{x-2≤0}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，A（-4，0），B（0，4），C，D分别为OB，OA的中点，E，F分别为AC，DB上一点，CE=AC，BD=BF，连接EF．
    （1）求直线EF的解析式；
    （2）求证：EF⊥AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知$\left\{\begin{array}{l}{3x+3y=m+1}\\{2x-y=m-1}\end{array}\right.$，若x＞y，求m的取值范围．

    查看答案和解析>>

    同步练习册答案