练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，点P、Q分别是BC、AC边上的点，PSAC，PRAB，若AQPQ，PR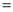PS，则下列结论：①ASAR；②QP∥AR；③△BRP ≌△CPS；④S四边形ARPQ=．其中正确的结论有____________（填序号）.

    ①② 【解析】连接AP. ∵PR=PS，AP=AP，PR⊥AB，PS⊥AC， ∴△APR≌△APS， ∴AS=AR，①正确. ∵PR=PS，PR⊥AB，PS⊥AC， ∴AP是∠BAC的平分线， ∴∠BAP=∠QAP. ∵AQ=PQ， ∴∠QAP=∠QPA， ∴∠BAP=∠QPA， ∴QP∥AR，②正确. 点P是BC的上的点，并...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：填空题

    已知点都在二次函数的图象上，则y1, y2 , y3的大小关系是______ 。

    【解析】试题分析：把A（4，y1），B（，y2），C（－2，y3）分别代入y＝(x－2)2－1得： y1＝(4－2)2－1＝3，y2＝(－2)2－1＝5－，y3＝(－2－2)2－1＝15， ∵5－＜3＜15， 所以y3＞y1＞y2． 故答案为：y3＞y1＞y2．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：解答题

    为倡导“低碳生活”，人们常选择以自行车作为代步工具，如图是一辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45 cm和60 cm，且它们互相垂直，座杆CE的长为20 cm，点A，C，E在同一条直线上，且∠CAB＝75°.(参考数据：sin 75°≈0.966，cos 75°≈0.259，tan 75°≈3.732)

    （1）求车架档AD的长；

    （2）求车座点E到车架档AB的距离(结果精确到1 cm)．

    （1）车架档AD的长是75 cm；（2）车座点E到车架档AB的距离约为63 cm. 【解析】试题分析：（1）在Rt△ACD中利用勾股定理求AD即可。 （2）过点E作EF⊥AB，在Rt△EFA中，利用三角函数求EF=AEsin75°，即可得到答案。 试题解析：(1)在Rt△ACD中，AC＝45 cm，DC＝60 cm， ∴AD＝＝75(cm)， ∴车架档AD的长是75 ...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：单选题

    在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，则下列式子一定成立的是(　　)

    A. a＝c·sin B B. a＝c·cos B C. b＝c·sin A D. b＝

    B 【解析】试题分析：本题可以利用锐角三角函数的定义代入求解即可．在Rt△ABC中，∠C=90°，则cosA=，sinA=，tanB=，cosB=，tanA=，cotA=，因而b=c•cosA=a•tanB，a=c•sinA=c•cosB=b•tanA=，所以，一定成立的是a=c•cosB． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    化简： ，然后在不等式的非负整数解中选择一个适当的数代入求值．

    原式=，当x=0时，原式=2 【解析】洪量分析：首先利用分式的混合运算法则将原式化简，然后解不等式，选择使得分式有意义的值代入求解即可求得答案． 【解答】【解析】 原式= = = = ∵不等式x≤2的非负整数解是0，1，2 ∵（x+1）（x-1）≠0，x+2≠0， ∴x≠±1，x≠-2， ∴把x=0代入＝2．

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    如图，△ABC是等边三角形，AD是角平分线，△ADE也是等边三角形，下列结论：①ADBC．②EFFD．③BEBD．④ACAE.其中正确的个数是（）

    A. 1 B. 2 C. 3 D. 4

    C 【解析】∵△ABC是等边三角形，△AED是等边三角形， ∴AB=AC=BC,∠BAC=60?,AE=AD=ED,∠EAD=60?， ∵∠DAB=∠DAC=30?， ∴AD⊥BC,故①正确；∠EAB=∠BAD=30?， ∴AB⊥ED，EF=DF，故②正确； ∴BE=BD，故③正确；∵AC=AE, ∴AC=AD, ∴∠C=∠ADC, ∵DAC=30?，∴∠C=7...

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    若一个三角形两边长分别是3、7，则第三边长可能是( )

    A. 4 B. 8 C. 10 D. 11

    B 【解析】设第三边长为x，则由三角形三边关系定理得7?3

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型：单选题

    将四个棱长为1的正方体如图摆放，则这个几何体的表面积是（　　）

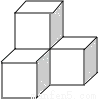
    A. 3 B. 9 C. 12 D. 18

    D 【解析】试题分析：观察几何体，得到这个几何体向前、向后、向上、向下、向左、向右分别有3个正方形，则它的表面积=6×3×1=18． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型：解答题

    阅读下列材料，然后解决问题：

    截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．

    (1)如图①，在△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．

    解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是 ；

    (2)问题解决：

    如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE＋CF＞EF；

    (3)问题拓展：

    如图③，在四边形ABCD中，∠B＋∠D＝180°，CB＝CD，∠BCD＝140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．

    (1) (2)证明见解析(3)BE＋DF＝EF 【解析】试题分析：（1）延长AD至E，使DE=AD，连接BE．由SAS证明△BDE≌△CDA，得出BE=AC=6，在△ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围； （2）延长FD至点G，使DG＝DF，连接BG，EG．同（1）得△BDG≌△CDF，得出BG＝CF，由线段垂直平分线的性质得出EF＝EG，在△BEG中...

    查看答案和解析>>

    同步练习册答案