分析:(1)根据折叠的性质有∠AED=∠A1ED,∠ADE=∠A1DE,∠A=∠A1,再根据三角形内角和定理得∠A1+∠A1ED+∠A1DE=180°,∠AED+∠A1ED+∠1=180°,∠ADE+∠A1DE+∠2=180°,则2∠A1+2∠A1ED+2∠A1DE=360°,2∠A1ED=180°-∠1,2∠A1DE=180°-∠2,易得2∠A1+180°-∠1+180°-∠2=360°,即可得到∠A1、∠1、∠2之间的数量关系;
(2)根据折叠的性质有∠AED=∠A2ED,∠A=∠A2,再根据三角形内角和定理得∠A2+∠A2ED+∠A2DE=180°,由三角形外角的性质有∠A2ED=∠1+∠BED=∠1+∠A+∠ADE,
即∠A2ED=∠1+∠A2+∠ADE,则有∠A2+∠1+∠A2+∠ADE+∠A2DE=180°,根据平角的定义得到∠ADE+∠A2DE=180°-∠2,代入上式即可得到∠A2、∠1、∠2之间的数量关系.
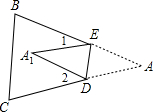
解答:解:(1)当点A落在△ABC内部时为点A1,
∵△AED由△A1ED沿ED折叠,
∴∠AED=∠A1ED,∠ADE=∠A1DE,∠A=∠A1,
∵∠A1+∠A1ED+∠A1DE=180°,
∴2∠A1+2∠A1ED+2∠A1DE=360°,
而∠AED+∠A1ED+∠1=180°,∠ADE+∠A1DE+∠2=180°,
∴2∠A1ED=180°-∠1,2∠A1DE=180°-∠2,
∴2∠A1+180°-∠1+180°-∠2=360°,
∴2∠A1=∠1+∠2;
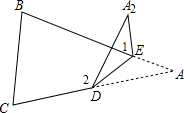
(2)当点A落在△ABC外部时为点A2,
∵△AED由△A2ED沿ED折叠,
∴∠AED=∠A2ED,∠A=∠A2,
∵∠A2+∠A2ED+∠A2DE=180°,
而∠A2ED=∠1+∠BED=∠1+∠A+∠ADE,
∴∠A2ED=∠1+∠A2+∠ADE,
∴∠A2+∠1+∠A2+∠ADE+∠A2DE=180°,
又∵∠2+∠ADE+∠A2DE=180°,即∠ADE+∠A2DE=180°-∠2,
∴2∠A2+∠1+180°-∠2=180°,
∴2∠A2=∠2-∠1.
故答案为2∠A1=∠1+∠2;2∠A2=∠2-∠1.
点评:本题考查了三角形内角和定理:三角形的内角和为180°.也考查了三角形外角的性质以及图形折叠的性质.




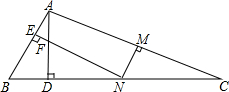 (2010•太原二模)如图,将△ABC纸片沿MN折叠后点C与点A恰好重合,设∠C=22.5°,AD⊥BC于点D.过点N作NE⊥AB于点E,并且交AD于点F,求证:DB=DF.
(2010•太原二模)如图,将△ABC纸片沿MN折叠后点C与点A恰好重合,设∠C=22.5°,AD⊥BC于点D.过点N作NE⊥AB于点E,并且交AD于点F,求证:DB=DF.