
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上一点,
上一点,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
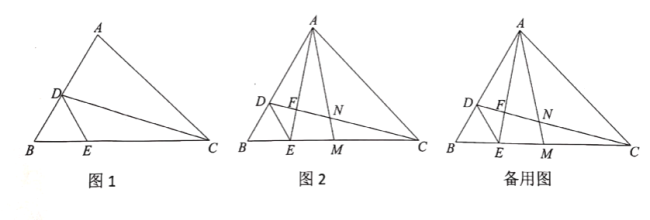
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
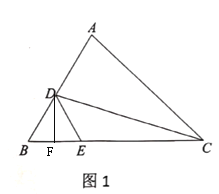
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,直接写出线段
,直接写出线段![]() ,
,![]() ,
,![]() 的等量关系.
的等量关系.
【答案】(1)9-![]() (2)见解析(3)AD+MC= AC,理由见解析.
(2)见解析(3)AD+MC= AC,理由见解析.
【解析】
(1)过点D作DF⊥BE,根据等边三角形的的性质求出DF的长,再利用勾股定理求出CF,即可求出EC的长;
(2)作AG=AB, 得到△ABG为等边三角形,先证明△ABE≌△AGM,再证明△AGC≌△CED,得到CG=DE,再根据MG=BE=DE即可求解;
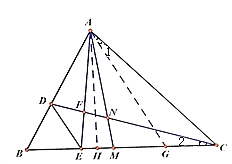
(3)作AH⊥BC,根据∠ACB=45°,∠BAC=75°,得到∠BAH=30°,∠HAC=45°设BH=x,
根据含30°的直角三角形与等腰直角三角形的性质分别表示出AD,MC,AC,即可求解.
(1)∵![]() ,
,![]() =
=![]()
∴△BDE为等边三角形,
作DF⊥BE,
∴EF=![]() BE=
BE=![]()
∴DF=![]()
∵CD=![]()
∴CF=![]() =9
=9
∴EC=CF-EF=9-![]() ;
;
(2)作AG=AB,∵∠B=60°,
∴△ABG为等边三角形,
∵AE=AM,∠ABE=∠AGM=60°,
∴△ABE≌△AGM,
∴∠ADC=60°+∠2=∠DAC=60°+∠1
故∠1=∠2,
∵∠AGC=120°=∠CED,AC=CD
∴△AGC≌△CED,
∴CG=DE,
又MG=BE=DE,
∴MC=MG+CG=2DE.
(3)∵∠ACB=45°,∠BAC=75°,
∴∠1=∠2=15°,
作AH⊥BC,∴∠BAH=30°,∠HAC=45°
设BH=x,
∴AB=2x,AH=![]() x=CH
x=CH
∴AC=![]() =
=![]() x,BC=(
x,BC=(![]() +1)x,
+1)x,
故CG=BC-BG=(![]() -1)x,BD=CG=(
-1)x,BD=CG=(![]() -1)x
-1)x
AD=AB-BD=(3-![]() )x
)x
CM=(2![]() -x)x
-x)x
∴AD+MC=(![]() +1)x=AC
+1)x=AC
即AD+MC= AC.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲.乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①100秒时乙到达终点;②a=8;③b=92④c=125,其中正确的是( )

A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,鲁能巴蜀中学团委决定组织同学们观看电影《我和我的祖国》,《中国机长》和《攀登者》,小明准备到电影院提前购票.已知三部电影单价之和为100元,计划购买三部电影票总共不超过135张;其中《攀登者》票价为30元,计划购买35张,《中国机长》至少购买25张,《我和我的祖国》数量不少于《中国机长》的2倍粗心的小明在做预算时将《我和我的祖国》和《中国机长》的票价弄反了,结果实际购买三种电影票时的总价比预算多了112元,若三部电影票的单价均为整数,则小明实际购买这三部电影票最多需要花费_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校对初2021级甲、乙两班各60名学生进行知识测试(满分60分),测试完成后分别抽取了12份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班12名学生测试成绩统计如下:
45,59,60,38,57,53,52,58,60,50,43,49
乙班12名学生测试成绩统计如下:
35,55,46,39,54,47,43,57,42,59,60,47
(整理数据)
按如下分数段整理,描述这两组样本数据
组别频数 |
|
|
|
|
|
甲 | 0 | 1 | 3 | 3 | 5 |
乙 | 2 | 2 | 3 | 1 | 4 |
(分析数据)
两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 |
甲 |
| 52.5 | |
乙 | 48.7 | 47 |
|
(1)![]() ,
,![]() ;
;
(2)若规定得分在40分及以上为合格,请估计乙班60名学生中知识测试合格的学生有多少人?
(3)你认为哪个班的学生知识测试的整体水平较好,请说明一条理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
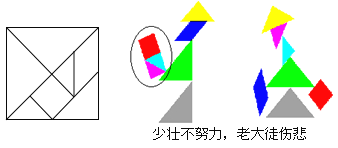
【题目】小明和小儿是同班同学,被分到了同一个学习小组,在一次数学活动课上,他们各自用一张面积为![]() 的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
少壮不努力,老大徒伤悲
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)求出点![]() ,点
,点![]() 的坐标.
的坐标.
(2)![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() 和
和![]() 的面积相等,求点
的面积相等,求点![]() 坐标.
坐标.
(3)如图2,平移直线![]() ,分别交
,分别交![]() 轴,
轴,![]() 轴于交于点
轴于交于点![]() ,
,![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,请直接写出所有符合条件的点
是等腰直角三角形?若存在,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
图1 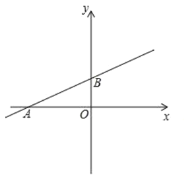 图2
图2 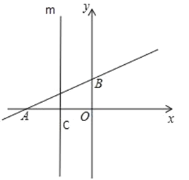
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°.
(1)用直尺和圆规作⊙O,使它经过A、B、D三点(保留作图痕迹);
(2)点C是否在⊙O上?请说明理由.
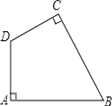
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图1所示的折叠椅.图2中的正方形ACBD是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.若正方形ACBD的面积为[9(2x-3y)2+12(2x-3y) (x+4y) +4(x+4y)2](米2)(x>y),你能求出这种折叠椅张开后的高度吗?
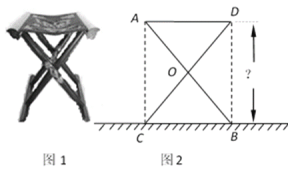
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com