
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P在函数y=$\frac{\sqrt{3}}{x}$(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,则当⊙P与坐标轴相切时,点P的坐标为($\sqrt{3}$,1)或(1,$\sqrt{3}$).
如图,点P在函数y=$\frac{\sqrt{3}}{x}$(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,则当⊙P与坐标轴相切时,点P的坐标为($\sqrt{3}$,1)或(1,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
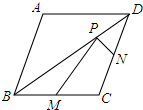 如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD的中点,点P是对角线上的一点,则PM+PN的最小值是$\frac{5}{2}$.
如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD的中点,点P是对角线上的一点,则PM+PN的最小值是$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
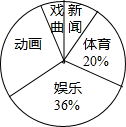 为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)| 节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
| 人数 | 36 | 90 | a | b | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | M<N | B. | M=N | C. | M>N | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com