类比联想:既然任意一个三角形的三边的垂直平分线交于一点,那三角形的三边上的中线是否也交于一点;三个角的平分线是否也交于一点;试通过折纸或用直尺、圆规画图验证这种猜想.
【答案】
分析:(1)根据题意画出图形,设△ABC的两条中线BD、CE相交于点G,连接AG并延长交BC于M,作BN∥CE,连接CN,由平行四边形的判定定理可判断出四边形BNCG是平行四边形,再由平行四边形的对角线互相平分即可得出结论;
(2)根据题意画出图形,由角平分线的性质判断出PF=PE即可.
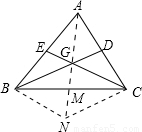
解答:解:(1)如图,设△ABC的两条中线BD、CE相交于点G,连接AG并延长交BC于M,作BN∥CE,连接CN,
∵E是AB的中点,BN∥CE,
∴点G是AN的中点,
∵点D是AC的中点,
∴GD∥CN,
∴四边形BNCG是平行四边形,
∴BC、GN互相平分,即点M是BC的中点,AM是BC的中线,即△ABC的三条中线交于一点;
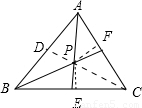
(2)如图,△ABC中,∠A、∠B的平分线交于点P,过P作AB、BC、AC的垂线,垂足分别为D、E、F,
∵AP、BP分别为∠A、∠B的平分线,
∴PF=PD=PE,
∵PF=PE,PE⊥BC,PF⊥AC,
∴点P在∠C的平分线上,
∴三角形的三个内角的角平分线相交于一点.
 点评:
点评:本题考查的是三角形的三个角平分线、三条边的中线交于一点的证明过程,是中学阶段必须掌握的知识点.





