
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

【答案】(1)∠EBC=30°;(2)△ABC的周长= 26.
【解析】
(1)根据等腰三角形的性质和三角形内角和定理求出∠ABC的度数,根据线段的垂直平分线的性质求出∠EBA的度数,计算即可;
(2)根据线段的垂直平分线的性质和三角形的周长公式求出AC+BC+AB=16+5+5=26,计算即可.
(1)∵AB=AC,∠A=40°,∴∠ABC=∠C=70°.
∵DE是AB的垂直平分线,∴EA=EB,∴∠EBA=∠A=40°,∴∠EBC=30°;
(2)∵DE是AB的垂直平分线,∴DA=BD=5,EB=AE,△EBC的周长=EB+BC+EC=EA+BC+EC=AC+BC=16,则△ABC的周长=AB+BC+AC=26.


科目:初中数学 来源: 题型:
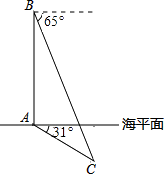
【题目】在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
(参考数据:sin31°≈ ![]() ,tan31°≈
,tan31°≈ ![]() ,sin65°≈
,sin65°≈ ![]() ,tan65°≈
,tan65°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用不等式表示下列关系:
(1)m与10的和不小于m的一半:________;
(2)3与x的5倍的差是非负数:________;
(3)长为a,宽为a-1的长方形的面积小于边长为a的正方形的面积:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七年级175名学生参加社会实践活动,已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.
(1)若学校单独租用这两种车,则各需多少元?
(2)若学校同时租用这两种客车共4辆(可以坐不满),而且比单独租用一种车节省租金,请你帮助该学校选择一种最节省租金的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A.当m=﹣3时,函数图象的顶点坐标是( ![]() )
)
B.当m>0时,函数图象截x轴所得的线段长度大于 ![]()
C.当m≠0时,函数图象经过同一个点
D.当m<0时,函数在x ![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形找出规律,并解答问题.
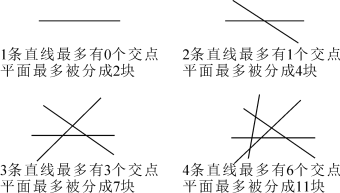
(1)5条直线相交,最多有_____个交点,平面最多被分成_____块;
(2)n条直线相交,最多有__________个交点,平面最多被分成____________块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1 , S2 . 若S=3,则S1+S2的值为( ) 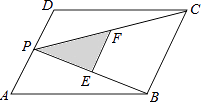
A.24
B.12
C.6
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com