
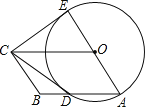
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
(1)求证:CD是⊙O的切线;
(2)若BC=3,AB=5,求平行四边形OABC的面积.
【答案】(1)见解析;(2)12
【解析】
(1)连接OD,证出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)求出CD,根据三角形的面积公式求出DF,根据平行四边形的面积公式求出即可.
∵CE是⊙O的切线,
∴∠OEC=90°,
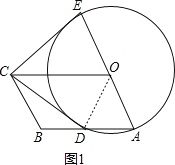
连接OD,如图1,
∵四边形OABC是平行四边形,
∴AO=BC,OC=AB,OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∵OD=OA,
∴∠A=∠ODA,
∴∠EOC=∠DOC,
在△EOC和△DOC中,
∵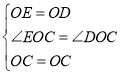 ,
,
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
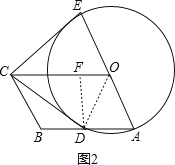
(2)过D作DF⊥OC于F,如图2,
∵四边形OABC是平行四边形,
∴OC=AB=5,OA=BC=3,
在Rt△CDO中,OC=5,OD=OA=3,
∴CD=![]() =4,
=4,
∵![]() ×CD×OD=
×CD×OD=![]() ×OC×DF,
×OC×DF,
∴DF=![]() =
=![]() ,
,
∴平行四边形OABC的面积=OC×DF=5×![]() =12.
=12.


科目:初中数学 来源: 题型:
【题目】某校为了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成如图所示两幅不完整的统计图,请根据统计图回答下列问题:
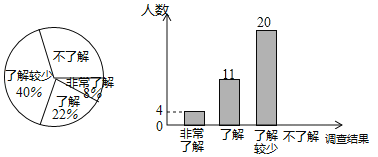
(1)补全条形统计图并填空,本次调查的学生共有 名,估计该校2000名学生中“不了解”的人数为 .
(2)“非常了解”的4人中有A1、A2两名男生,B1、B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直半径OA,C为垂足,DE=6,连接DB,![]() ,过点E作EM∥BD,交BA的延长线于点M.
,过点E作EM∥BD,交BA的延长线于点M.

(1)求的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
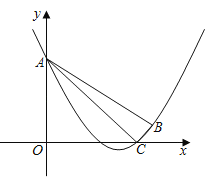
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
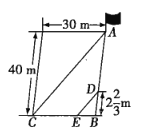
【题目】如图,在一个长40m,宽30m的长方形小操场上,王刚从A点出发,沿着A→B→C的路线以3m/s的速度跑向C地.当他出发4s后,张华有东西需要交给他,就从A地出发沿王刚走的路线追赶,当张华跑到距B地![]() m的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上.此时,A处的小旗在阳光下的影子也恰好落在对角线AC上.求:
m的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上.此时,A处的小旗在阳光下的影子也恰好落在对角线AC上.求:
(1)他们的影子重叠时,两人相距多少米(DE的长)?
(2)张华追赶王刚的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
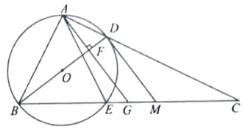
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点.连接
中点.连接![]() .作
.作![]() ,垂足为
,垂足为![]() ,
,![]() 的外接圆
的外接圆![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作圆
作圆![]() 的切线,交
的切线,交![]() 于点
于点![]() .若
.若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
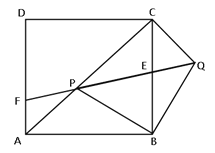
【题目】如图,等腰Rt△BPQ的顶点P在正方形ABCD的对角线AC上(P与AC不重合),∠PBQ=90°,QP与BC交于E,QP延长线交AD于F,连CQ.
(1)①求证:AP=CQ ;
②求证:![]()
(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
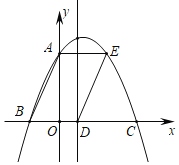
【题目】如图,抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com