
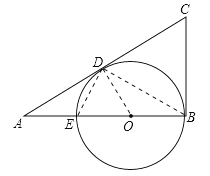
【题目】如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2![]() , 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
, 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
(1)求⊙O的半径.
(2)求CD的长.
【答案】解:(1)连接OD、DE、DB,设⊙O半径为r,
∵CD为⊙O切线,∴∠ODA=90°,
∵BE为⊙O直径,∴∠BDE=90°,
∴∠ADE=∠BDO,
∵OB=OD,∴∠OBD=∠ODB,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴![]() ,
,
∴ABAE=![]() ,
,
∵AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根,
∴k=12,
解方程x2﹣8x+12=0得:两个实数根为:2和6,
∴设半径的长为r,
可得半径r=![]() ×(6﹣2)=2;
×(6﹣2)=2;
(2)∵∠B=90°,
∴CB为⊙O切线,
∴CD=CB,
∴CB2+AB2=AC2 ,
∴CD2+62=(2![]() +CD)2 ,
+CD)2 ,
∴CD=2![]() .
.
答:CD的长度为2![]() .
.
【解析】(1)根据切线长定理得出ABAE的长=12,进而得出k的值,设半径的长为r,再代入切线长定理解答即可;
(2)根据切线长定理,即可得出CD=CB,由勾股定理得CD的长即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源: 题型:
【题目】没有水就没有生命.地球上的总储量中97%是咸水,余下的是淡水,其中可直接饮用的只有0.5%,大约有105万亿吨,约占淡水总量的![]() , 其余淡水资源集中在两极冰川中,难以利用.目前,世界上近20%的人缺少饮用水,我国的形势也十分严峻,人均可用淡水量比世界人均可用淡水量少25%.
, 其余淡水资源集中在两极冰川中,难以利用.目前,世界上近20%的人缺少饮用水,我国的形势也十分严峻,人均可用淡水量比世界人均可用淡水量少25%.
(1)世界上可用淡水量占淡水总量的百分之几;
(2)世界上只有百分之几的人口不缺饮用水;
(3)我国人均可用淡水量相当于世界人均可用淡水量的百分之几;
(4)世界上的水资源总储量大约为多少万亿吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
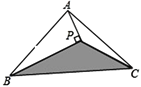
A. 3cm2 B. 4cm2 C. 5cm2 D. 6cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
(1)求证:BC平分∠DBA;
(2)若CD=6,BC=10,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2015的值为( )
A. ﹣2015 B. ﹣2014 C. ﹣1007 D. ﹣1008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.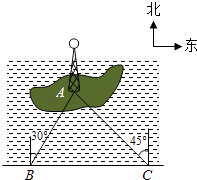
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com