
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是平行四边形,点
是平行四边形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的动点,若
上的动点,若![]() 是等腰三角形,则点
是等腰三角形,则点![]() 的坐标为_____.
的坐标为_____.

【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
分三种情形讨论求解即可:①当EP=EB时,②当BP=BE时,③当PB=PE时.
解:①当EP=EB时,
如图1,作EH⊥AD于H,则四边形OAHE是矩形.
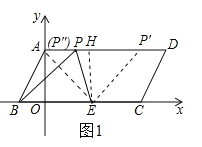
∵![]() ,
,![]() ,
,![]() ,
,
∴OA=EH=2,BC=5,
∵点![]() 是
是![]() 的中点,
的中点,
∴BE=2.5,OE=AH=1.5,
PH=![]() =1.5,
=1.5,
当点P在点H左侧时,P″(0,2),当点P在点H右侧时,P′(3,2);
②当BP=BE时,
如图2,作PF⊥BC于F,则四边形OAPF是矩形,
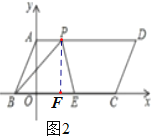
∵![]() ,
,![]() ,
,![]() ,
,
∴OA=PF=2,BC=5,
∵点![]() 是
是![]() 的中点,
的中点,
∴BE=2.5,OE =1.5,
∴OF=AP=0.5,
∴P(0.5,2);
③当PB=PE时,如图2,
∵PB=PE,PF⊥BC,
∴BF=![]() =1.25,
=1.25,
∴OF=0.25,
∴P(0.25,2);
综上所述,满足条件的点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】计算或化简
(1)|﹣1|+(﹣2)3+(7﹣π)0﹣![]()
(2)3a32a6﹣3a12÷a3
(3)(x+y)2+(x﹣y)(x+2y)
(4)(3a+b﹣2)(3a﹣b+2)
(5)(3a+2)2(3a﹣2)2
(6)7862﹣786×172+862
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,过直线AC上一点G作y轴的平行线交抛物线一点F,是否存在点F,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三个关于x的一元二次方程ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0恰有一个公共根,则 ![]() 的值为( )
的值为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的一条边
的一条边![]() 的长为5,另两边
的长为5,另两边![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根.
的两个实数根.
(1)求证:无论![]() 为何值,方程总有两个不相等的实数根;
为何值,方程总有两个不相等的实数根;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形,并求出
为直角三角形,并求出![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:![]()
⑴根据如图1,写出一个等式:
⑵如图2,若长方形的长AB为10,AD宽为6,分别求a、b的值;
⑶如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=6,ab=10,请求出阴影部分的面积.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com