


分析 观察计算:(1)由题意可以得知管道长度为d1=PB+BA(km),根据BP⊥l于点P得出PB=2,故可以得出d1的值为a+2.
(2)由条件根据勾股定理可以求出KB的值,由轴对称可以求出A′K的值,在Rt△KBA′由勾股定理可以求出A′B的值$\sqrt{{a}^{2}+24}$就是管道长度.
探索归纳:(1)①把a=4代入d1=a+2和d2=$\sqrt{{a}^{2}+24}$就可以比较其大小;
②把a=6代入d1=a+2和d2=$\sqrt{{a}^{2}+24}$就可以比较其大小;
(2)分类进行讨论当d1>d2,d1=d2,d1<d2时就可以分别求出a的范围,从而确定选择方案.
解答 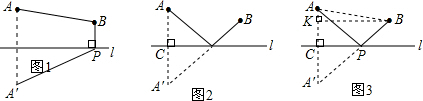 解:(1)∵如图1,作A关于执行l的对称点A′,连接PA′,
解:(1)∵如图1,作A关于执行l的对称点A′,连接PA′,
∵A和A'关于直线l对称,
∴PA=PA',
d1=PB+BA=PB+PA'=a+2;
故答案为:a+2;
(2)因为BK2=a2-1,
A'B2=BK2+A'K2=a2-1+52=a2+24
所以d2=$\sqrt{{a}^{2}+24}$;
故答案为:$\sqrt{{a}^{2}+24}$;
探索归纳:
(1)①当a=4时,d1=6,d2=$\sqrt{40}$,d1<d2;
②当a=6时,d1=8,d2=$\sqrt{60}$,d1>d2;
故答案为:<,>;
(2)d12-d22=(a+2)2-($\sqrt{{a}^{2}+24}$)2=4a-20.
①当4a-20>0,即a>5时,d12-d22>0,
∴d1-d2>0,
∴d1>d2;
②当4a-20=0,即a=5时,d12-d22=0,
∴d1-d2=0,
∴d1=d2
③当4a-20<0,即a<5时,d12-d22<0,
∴d1-d2<0,
∴d1<d2
综上可知:当a>5时,选方案二;
当a=5时,选方案一或方案二;
当1<a<5时,选方案一.
点评 本题考查了轴对称的性质的运用,最短路线问题数学模式的运用,勾股定理的运用,数的大小的比较方法的运用,综合考查了学生的作图能力,运用数学知识解决实际问题的能力,以及观察探究和分类讨论的数学思想方法.


科目:初中数学 来源: 题型:填空题
 如图,AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线交于点D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=3,FB=1,EF=$\frac{3}{2}$,则线段CD的长为$\frac{4}{3}$.
如图,AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线交于点D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=3,FB=1,EF=$\frac{3}{2}$,则线段CD的长为$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com