
【题目】如图,在矩形ABCD中,AB=6,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,点C的对应点为点F,连接AF,若
,E为CD边上一点,将△BCE沿BE折叠,点C的对应点为点F,连接AF,若![]() ,则CE=__________.
,则CE=__________.

【答案】![]()
【解析】
已知![]() ,可作辅助线构造直角三角形,设未知数,利用勾股定理可求出FM、BM,进而求出FN,再利用三角形相似和折叠的性质求出EC.
,可作辅助线构造直角三角形,设未知数,利用勾股定理可求出FM、BM,进而求出FN,再利用三角形相似和折叠的性质求出EC.
解:过点F作MN∥AD,交AB、CD分别于点M、N,则MN⊥AB,MN⊥CD,
∴∠FNE=∠BMF=90°
∴∠NFE+∠NEF=90°
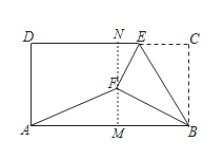
由折叠得:EC=EF,BC=BF=![]() ,∠C=∠BFE=90°,
,∠C=∠BFE=90°,
∴∠NFE+∠BFM=90°
∴∠MFB=∠NEF
∵![]()
∴设FM=x,则AM=3x,![]() ,
,
∴![]()
在Rt△BFM中,由勾股定理得:![]()
解得:![]()
∵![]()
∴x=1
∴FM=1,AM=BM=3,
∵∠FNE=∠BMF=90°, ∠MFB=∠NEF
∴△BMF∽△FNE,
∴![]()
∴![]()
∴EF=![]()
故答案为: ![]()


科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,要求被调查的市民必选且只能选一项.根据调查结果绘制了如图尚不完整的扇形统计图,其中将“手机上网”和“电脑上网”作为“获取新闻的最主要途径”的市民分别有600人和510人,并且扇形统计图中![]() ,
,![]() 满足
满足![]() .请根据所给信息,解答下列问题:
.请根据所给信息,解答下列问题:

(1)请计算扇形统计图中“电脑上网”所在扇形的圆心角的度数;
(2)求扇形统计图中![]() ,
,![]() 的值;
的值;
(3)若该市约有200万人,请你估计其中将“手机上网”和“报纸”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
(1)求抛物线的解析式;
(2)设点M(1,m),当MB+MD的值最小时,求m的值;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;
(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 中,D是
中,D是![]() 上一点,连接
上一点,连接![]() 并将
并将![]() 绕点A逆时针旋转120°得到线段
绕点A逆时针旋转120°得到线段![]() ,连接
,连接![]() 交
交![]() 于点F.
于点F.
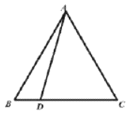
(1)当点D为![]() 中点,且
中点,且![]() 时,
时,![]() ___________;
___________;
(2)补全图形,探究线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
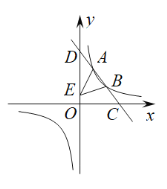
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中(小正方形的边长为1个单位长度),点![]() ,
,![]() ,
,![]() 都在格点上,以
都在格点上,以![]() 为坐标原点建立平面直角坐标系.
为坐标原点建立平面直角坐标系.
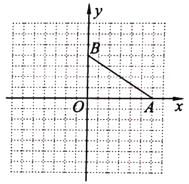
(1)分别写出点![]() ,
,![]() 的坐标:________,画出线段
的坐标:________,画出线段![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 的线段
的线段![]() ;
;
(2)若线段![]() 的中点
的中点![]() 在反比例函数
在反比例函数![]()
![]() 的图象上,则
的图象上,则![]() 的值为________.(直接写出答案)
的值为________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A1(1,![]() ),A2(
),A2(![]() ,
,![]() ),A3(2,
),A3(2,![]() ),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
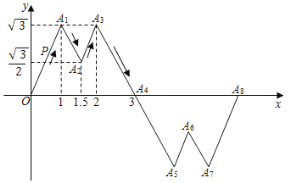
A.(1010,![]() )B.(2020,
)B.(2020,![]() )C.(2016,0)D.(1010,
)C.(2016,0)D.(1010,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com