【题目】下面是小明做的一道题目以及他的解题过程：
题目：在同一平面上，若∠BOA＝75°，∠BOC＝22°，求∠AOC的度数，
解：根据题意可画图，如图所示，AOC＝∠BOA－∠BOC＝75°－22°＝53°.
如果你是老师，能判小明满分吗？若能，请说明理由，若不能，请将错误指出来，并给出你认为正确的解法．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】计算．
（1）﹣7+13﹣6+20
（2）3+（﹣2）﹣3×（﹣5）×0
（3）16÷（﹣2）3﹣（﹣
）×（﹣4）
（4）﹣36×（
）
（5）（2a2﹣1+2a）﹣（a﹣1+a2）．
（6）8a+2b﹣2（5a﹣2b）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，O是直线AB上的一点，∠COD是直角，OE平分∠BOC.
(1)如图1.
①若∠AOC＝60°，求∠DOE的度数；
②若∠AOC＝α，直接写出∠DOE的度数(用含α的式子表示)；
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置，试探究∠DOE和∠AOC的度数之间的关系，写出你的结论，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：
一艘船从甲码头到乙码头顺流而行，用了2.5h；从乙码头返回甲码头逆流而行，用了3h．已知水流的速度是3.5km/h，求船在静水中的平均速度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦。我国西汉《周髀算经》中周公与商高对话中涉及勾股定理，所以这个定理也有人称商高定理，勾股定理在西方被称为毕达哥拉斯定理，相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。
我们知道，可以用一个数表示数轴上的一个点，而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴，同时，增加一个垂直于x轴的数轴，叫做y轴，如下图。这样，我们可以用一组数对来表示平面上的一个点，同时，平面上的一个点也可以用一组数对来表示，比如下图中A点的位置可以表示为（2，3），而数对（2，3）所对应的点即为A。若平面上的点M 
，N 
，我们定义点M、N在x轴方向上的距离为： 
，点M、N在y轴方向上的距离为： 
。例如，点G（3，4）与点H（1，-1）在x轴方向上的距离为：|3-1|=2，点M、N在y轴方向上的距离为：|4-（-1）|=5。
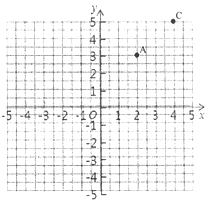
（1）若点B位置为（-1，-1），请在图中画出点B；图中点C的位置用数对______来表示。
（2）在（1）条件下，A、B两点在x轴方向上的距离为________，在y轴方向上的距离为_______，A、B两点间的距离为______；若E点、F点的位置分别为（a，b）、（c，d），点E、F之间的距离为|EF|，则
=_______________。
（3）有一个点D，它与（0，0）点的距离为1，请画出D点所有可能的位置。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
