
【题目】正方形ABCD和正方形CEFG如图1所示,其中B、C、E在一条直线上,O是AF的中点,连接OD、OG
(1)探究OD与OG的位置关系![]() 的值;(写出结论不用证明)
的值;(写出结论不用证明)
(2)如图2所示,将正方形ABCD和正方形CEFG改为菱形ABCD和菱形CEFG,且∠ABC=∠DCE=120°,探究OD与OG的位置关系,及![]() 的比值;
的比值;
(3)拓展探索:把图1中的正方形CEFG绕C顺时针旋转小于90°的角后,其他条件均不变,问第1问中的两个结论是否发生变化?(写出结论不用证明)

【答案】(1)OD⊥OG. ![]() =1;(2)OD⊥OG,
=1;(2)OD⊥OG, ![]() ,理由见解析;(3)第(1)问中的两个结论没有发生变化.
,理由见解析;(3)第(1)问中的两个结论没有发生变化.
【解析】试题分析:
(1)延长GO交AD于点H,由已知条件易证△AHO≌△FGO,从而可得GO=HO,GF=AH=GC,结合AD=CD可得DH=DG,结合∠GDH=90°即可得到OD⊥OG,OD=OG,从而可得![]() ;
;
(2)延长GO交AD于H,同(1)易证△AHO≌△FGO,从而同理可得OD⊥OG,由已知条件可证得∠ODG=60°,则∠DGO=30°,结合∠DOG=90°,即可得到tan∠DGO=![]() ;
;
(3)第(1)问中的两个结论没有发生变化,如图3,过点F作FH∥AD交DO的延长线于点H,延长DC交FH于点M,连接GH,DG,这样由已知易证△ADO≌△FHO,从而可得FH=AD=CD,DO=HO;再由∠GCE=∠CMN=∠E=∠EFG=90°,可得∠DCG+∠MCN=∠MCN+∠CNM=∠FNE+∠NEF=∠NEF+∠GFH=90°,结合∠CNM=∠FNE可得∠DCG=∠CNM=∠GFH即可证得△DCG≌△HFG,进一步即可证得△DGH是等腰直角三角形,即可由此得到DO=GO,且DO⊥GO,从而说明(1)中结论仍然成立了.
试题解析:
(1)OD⊥OG, ![]() =1,理由如下:
=1,理由如下:
如图1,延长GO交AD于点H,由已知可得OA=OF,AD∥GF,
∴∠OAH=∠OFG,∠AHO=∠FGO,
∴△AHO≌△FGO,
∴OH=OG,AH=GF=GC,
又∵AD=CD,
∴DH=DG,
∴DO⊥OG,
∵∠ADC=90°,∴DO=OG,
∴![]() ;
;

(2)OD⊥OG , ![]() ,理由如下:
,理由如下:
如图2所示,延长GO交AD于H.

∵菱形ABCD和菱形CEFG,且B、C、E在一条直线上,
∴AD∥GF,
∵O是AF的中点,
∴△AOH≌△FOG,
∴AH=CF,HO=OG,
∵CF=CG,AD=CD,
∴DH=DG,
∴DO⊥HG且∠ODG=60°,
∴![]() ;
;
(3)第(1)问中的两个结论没有发生变化,理由如下:
如图3,过点F作FH∥AD交DO的延长线于点H,延长DC交FH于点M,连接GH,DG,
∴∠ADO=∠FHO,∠DAO=∠HFO,
又∵AO=FO,
∴△ADO≌△FHO,
∴FH=AD=CD,DO=HO,
∵∠GCE=∠CMN=∠E=∠EFG=90°,
∴∠DCG+∠MCN=∠MCN+∠CNM=∠FNE+∠NEF=∠NEF+∠GFH=90°,
又∵∠CNM=∠FNE,
∴∠DCG=∠CNM=∠GFH,
又∵DC=FH,CG=FG,
∴△DCG≌△HFG,
∴DG=HG/span>,∠DGC=∠HGF,
∵∠CGH+∠HFG=∠CGF=90°,
∴∠CGH+∠DGC=∠=90°,
∴△DGH是等腰直角三角形,
又∵DO=HO,
∴DO=GO,且DO⊥GO,
∴![]() ,
,
∴(1)中结论仍然成立.



科目:初中数学 来源: 题型:
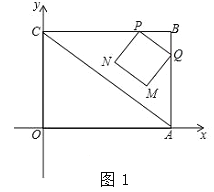
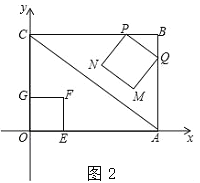
【题目】已知矩形OABC在如图所示平面直角坐标系中,点B的坐标为(4,3),连接AC.动点P从点B出发,以2cm/s的速度,沿直线BC方向运动,运动到C为止(不包括端点B、C),过点P作PQ∥AC交线段BA于点Q,以PQ为边向下作正方形PQMN,设正方形PQMN与△ABC重叠部分图形面积为S(cm2),设点P的运动时间为t(s).
(1)请用含t的代数式表示BQ长和N点的坐标;
(2)求S与t之间的函数关系式,并指出t的取值范围;
(3)如图2,点G在边OC上,且OG=1cm,在点P从点B出发的同时,另有一动点E从点O出发,以2cm/s的速度,沿x轴正方向运动,以OG、OE为一组邻边作矩形OEFG.试求当点F落在正方形PQMN的内部(不含边界)时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有点A、点O和直线PQ,其中网格正方形的边长为1个单位,在网格中完成下列画图.(不必写出画法,保留画图痕迹,并写出结论)

(1)将点A向右平移3个单位可到达点B,再向上平移2个单位可到达点C,标出点B、点C,并联结AB、BC和AC,画出三角形ABC;
(2)画出三角形ABC关于直线PQ的轴对称的图形;
(3)画出三角形ABC关于点O的中心对称的图形.
结论:
(1) ;
(2)三角形 是三角形ABC关于直线PQ的轴对称的图形;
(3)三角形 是三角形ABC关于点O的中心对称的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
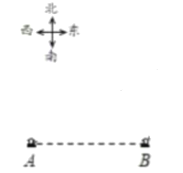
【题目】如图,A地和B地都是海上观测站,B地在A地正东方向,且A、B两地相距2海里. 从A地发现它的北偏东60°方向有一艘船C,同时,从B地发现船C在它的北偏东30°方向.
(1)在图中画出船C所在的位置;(要求用直尺与量角器作图,保留作图痕迹)
(2)已知三角形的内角和等于180°,求∠ACB的度数.
(3)此时船C与B地相距______海里.(只需写出结果,不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
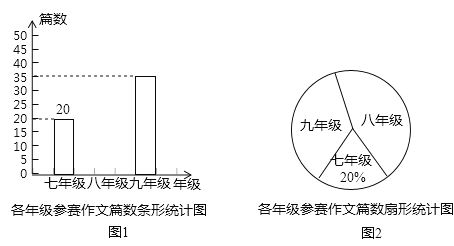
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC 的边OC 、OA 分别与 x 轴、 y 轴重合, AOC 90,BCO 45, AB // OC , BC 6 ![]() ,点C 的坐标为 9,0.
,点C 的坐标为 9,0.
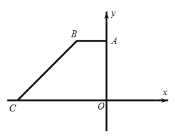

(1)求点 B 的坐标;
(2)若直线 DE 交四边形的对角线 BO 于点 D ,交 y 轴于点 E ,且OE 2 , OD 2BD ,求:
① ODE 的面积;
②点 D 的坐标.
(3)在(2)的条件下,坐标平面内是否存在点 P ,使以O 、E 、P 、D 为顶点的四边形是平行四边形? 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在∠A内部有一点P,连接BP、CP,请回答下列问题:

(1)求证:∠P=∠1+∠A+∠2;
(2)如图2,利用上面的结论,在五角星中,∠A+∠B+∠C+∠D+∠E= ;
(3)如图3,如果在∠BAC间有两个向上突起的角,请你根据前面的结论猜想∠1、∠2、∠3、∠4、∠5、∠A之间有什么等量关系,直接写出结论即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交AC于点D,动点P在抛物线对称轴上,动点Q在抛物线上.
(1)求抛物线的解析式;
(2)当PO+PC的值最小时,求点P的坐标;
(3)是否存在以A,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com