练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一张正方形纸片ABCD，第一次对折，使BC与AD重合，得到折痕EF(如图(a))；第二次对折使DF与AE重合(如图(b))；第三次对折，沿对角线AO对折，使E与G重合，此时用剪刀沿GH剪掉△AGH，其中OH＝OG，然后展开展平(如图(c))．

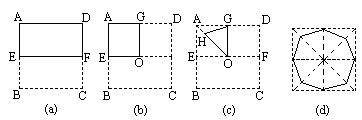
    (1)你得到了一个什么图形？

    (2)它是轴对称图形吗？

    (3)它是旋转对称图形吗？如是，请指出旋转中心和旋转角？

    (4)它是中心对称图形吗？

    答案：
    解析：

    　　(1)正八边形

    　　(2)是轴对称图形

    　　(3)是旋转对称图形，

    　　(4)是中心对称图形


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

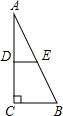    精英家教网如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有两个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、如图①，将一张直角三角形纸片△ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形；再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”．
    （1）如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；
    （2）如图③，在正方形网格中，以给定的BC为一边，画出一个斜三角形ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；
    （3）若一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

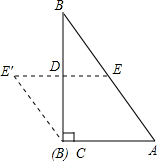    如图，将一张直角三角形纸片ABC沿中位线DE剪开后在平面上将△BDE绕着CB的中点D逆时针旋转180°，点E到了点E′位置，则四边形ACE′E的形状是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）数学课上，老师出了一道题，如图①，Rt△ABC中，∠C=90°，AC=
    12
    AB    ，求证：∠B=30°，请你完成证明过程．
    （2）如图②，四边形ABCD是一张边长为2的正方形纸片，E、F分别为AB、CD的中点，沿过点D的抓痕将纸片翻折，使点A落在EF上的点A′处，折痕交AE于点G，请运用（1）中的结论求∠ADG的度数和AG的长．
    （3）若矩形纸片ABCD按如图③所示的方式折叠，B、D两点恰好重合于一点O（如图④），当AB=6，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在长为44，宽为12的矩形PQRS中，将一张直角三角形纸片ABC和一张正方形纸片DEFG如图放置，其中边AB、DE在PQ上，边EF在QR上，边BC、DG在同一直线上，且Rt△ABC两直角边BC=6，AB=8，正方形DEFG的边长为4．从初始时刻开始，三角形纸片ABC，沿AP方向以每秒1个单位长度的速度向左平移；同时正方形纸片DEFG，沿QR方向以每秒2个单位长度的速度向上平移，当边GF落在SR上时，纸片DEFG立即沿RS方向以原速度向左平移，直至G点与S点重合时，两张纸片同时停止移动．设平移时间为x秒．
    （1）请填空：当x=2时，CD=
    2
    		2
    2
    		2
    ，DQ=
    4
    		2
    4
    		2
    ，此时CD+DQ
    =
    =
    CQ（请填“＜”、“=”、“＞”）；
    （2）如图2，当纸片DEFG沿QR方向平移时，连接CD、DQ和CQ，求平移过程中△CDQ的面积S与x的函数关系式，并写出自变量x的取值范围（这里规定线段的面积为零）；
    （3）如图3，当纸片DEFG沿RS方向平移时，是否存在这样的时刻x，使以A、C、D为顶点的三角形是等腰三角形？若存在，求出对应x的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案