
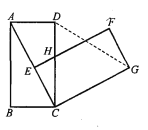
【题目】如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG.
(1)CH= .
(2)求DG的长.
【答案】(1) ![]() ;(2)
;(2)![]() ;
;
【解析】
试题分析:(1)利用勾股定理列式求出AC,根据旋转的性质可得CE=BC,然后根据△ABC和△CEH相似,利用相似三角形对应边成比例列式求解即可;
(2)过点G作GM⊥CD于M,然后求出△ABC和△GMC相似,根据相似三角形对应边成比例求出CM、MG,再求出DM,然后利用勾股定理列式计算即可得到DG.
试题解析:(1)在矩形ABCD中,∵AB=4,BC=3,
∴AC=![]() ,
,
∵矩形ABCD绕点C按顺时针方向旋转得矩形CEFG,
∴CE=BC=3,
∵∠BAC+∠ACB=90°,∠ECH+∠ACB=90°,
∴∠BAC=∠ECH,
又∵∠B=∠CEH=90°,
∴△ABC∽△CEH,
∴![]() ,
,
即![]()
解得![]() ;
;
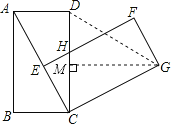
(2)如图,过点G作GM⊥CD于M,
∵∠ACB+∠ACD=∠GCM+∠ACD=90°,
∴∠ACB=∠GCM,
又∵∠B=∠GMC=90°,
∴△ABC∽△GMC,
∴![]() ,
,
即![]() ,
,
解得CM=![]() ,MG=
,MG=![]() ,
,
∴DM=CD-CM=4-![]() =
=![]() ,
,
在Rt△DMG中,DG=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2 , 长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由. 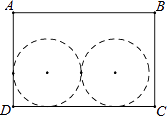
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点如图1) 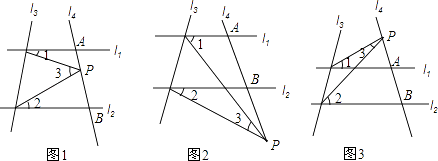
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
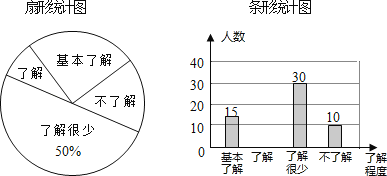
(1)接受问卷调查的学生共有___名,扇形统计图中“基本了解”部分所对应扇形的圆心角为___;请补全条形统计图;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校20名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件5个或乙种零件4个,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元,若要使车间每天获利不低于1 800元,至少要派( )名同学加工乙种零件.
A. 11 B. 12 C. 13 D. 14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com