
【题目】(1)如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内.
解:如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴ =AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4, =∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC= °
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
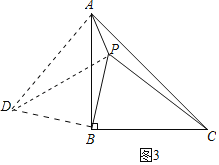
(2)如图3,在△ABC中,AB=BC,∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.
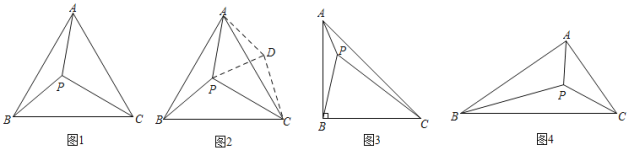
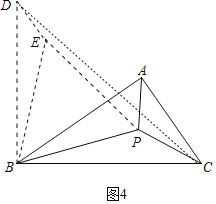
(3)拓展应用.如图4,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .
【答案】(1)PD,∠CAD,∠APB,90;(2)∠APB=135°;(3)![]() .
.
【解析】
(1)根据全等三角形的判定和性质即可解决问题;
(2)图3中,把△PBC绕B点逆时针旋转90°得到△DBA,利用勾股定理的逆定理证明∠APD=90°即可解决问题;
(3)如图4中,将△ABP绕着点B逆时针旋转60°,得到△DBE,证明△ABP≌△DBE,则∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,再证明∠DBC=90°,在Rt△BCD中,由勾股定理求出CD的长度,即为PA+PB+PC的最小值.
(1)如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴PD=AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°,
∴∠BAP=∠CAD,
∴△ABP≌△ACD(SAS)
∴BP=CD=4,∠APB=∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC=90°
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
故答案为:PD,∠CAD,∠APB,90.
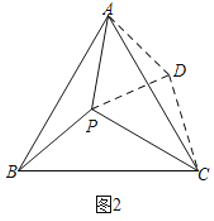
(2)解:∵∠ABC=90°,BC=AB,
∴把△PBC绕B点逆时针旋转90°得到△DBA,如图3,
∴AD=PC=3,BD=BP=2,
∵∠PBD=90°
∴DP=![]() PB=2
PB=2![]() ,∠DPB=45°,
,∠DPB=45°,
在△APD中,AD=3,PD=2![]() ,PA=1,
,PA=1,
∵12+(2![]() )2=32,
)2=32,
∴AP2+PD2=BD2,
∴△APD为直角三角形,
∴∠APD=90°,
∴∠APB=∠APD+∠DPB=90°+45°=135°.
(3)解:如图4中,将△ABP绕着点B逆时针旋转60°,得到△DBE,连接EP,CD,
∴△ABP≌△DBE
∴∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,
∴△BPE是等边三角形
∴EP=BP
∴AP+BP+PC=PC+EP+DE
∴当点D,点E,点P,点C共线时,PA+PB+PC有最小值CD
∵∠ABC=30°=∠ABP+∠PBC
∴∠DBE+∠PBC=30°
∴∠DBC=90°
∴CD=![]() ,
,
故答案为![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
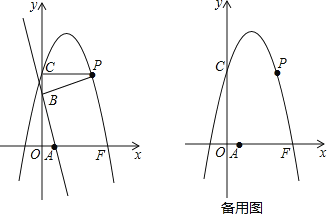
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c与直线y=c分别交y轴的正半轴于点C和第一象限的点P,连接PB,得△PCB≌△BOA(O为坐标原点).若抛物线与x轴正半轴交点为点F,设M是点C,F间抛物线上的一点(包括端点),其横坐标为m.
(1)直接写出点P的坐标和抛物线的解析式;
(2)当m为何值时,△MAB面积S取得最小值和最大值?请说明理由;
(3)求满足∠MPO=∠POA的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近诸暨城市形象宣传片《西施故里好美诸暨》正式发布,此篇历时6个月拍摄,从不同角度向世界介绍了诸暨,现有一个不透明的口袋装有分别标有汉字“好”、“美”、“诸”、“暨”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字“美”的概率是多少.
(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图或列表的方法,求出甲取出的两个球上的汉字恰能组成“诸暨”的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
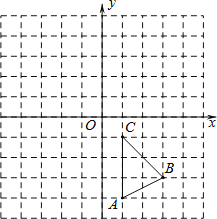
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣4)、B(3,﹣3)、C(1,﹣1)(每个小方格都是边长为一个单位长度的正方形).
(1)请画出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元二次方程,把它转化为两个一元一次方程来解,求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验,各类方程的解法不尽相同,但是它们有一个共同的基本数学思想“转化”,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.
例如:解方程![]()
解:移项,得![]()
两边平方,得![]()
即![]()
两边再平方,得![]()
即![]()
解这个方程得:![]()
检验:当![]() 时,原方程左边
时,原方程左边![]() ,右边
,右边![]()
![]() 不是原方程的根;
不是原方程的根;
当![]() 时,原方程左边
时,原方程左边![]() ,右边
,右边![]()
![]() 原方程的根
原方程的根
![]() 原方程的根是
原方程的根是![]() .
.
(1)请仿照上述解法,求出方程![]() 的解;
的解;
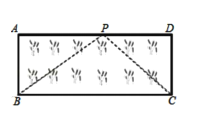
(2)如图已知矩形草坪![]() 的长
的长![]() ,宽
,宽![]() ,小华把一根长为
,小华把一根长为![]() 的绳子的一端固定在点
的绳子的一端固定在点![]() ,从草坪边沿
,从草坪边沿![]() 走到点
走到点![]() 处,把长绳
处,把长绳![]() 段拉直并固定在点
段拉直并固定在点![]() ,然后沿草坪边沿
,然后沿草坪边沿![]() 走到点
走到点![]() 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点
处,把长绳剩下的一段拉直,长绳的另一端恰好落在点![]() ,则
,则![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )
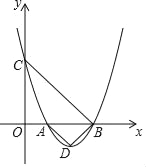
A. 2 B. ﹣2或﹣4 C. ﹣2 D. ﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com