
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄ¶ž“ĪŗÆŹży=ax2-(2a+2)x+b(a”Ł0)ŌŚx=0ŗĶx=6Ź±ŗÆŹżÖµĻąµČ.
(1)ĒóaµÄÖµ;
(2)Čōøƶž“ĪŗÆŹżµÄĶ¼ĻóÓėÖ±Ļßy=-2xµÄŅ»øö½»µćĪŖ(2,m),ĒóĖüµÄ½āĪöŹ½;
(3)ŌŚ(2)µÄĢõ¼žĻĀ,Ö±Ļßy=-2x-4ÓėxÖį,yÖį·Ö±š½»ÓŚA,B,½«Ļ߶ĪABĻņÓŅĘ½ŅĘn(n>0)øöµ„Ī»,Ķ¬Ź±½«øƶž“ĪŗÆŹżŌŚ2”Üx”Ü7µÄ²æ·ÖĻņ×óĘ½ŅĘnøöµ„Ī»ŗóµĆµ½µÄĶ¼Ļó¼ĒĪŖG,Ēė½įŗĻĶ¼ĻóÖ±½Ó»Ų“š,µ±Ķ¼ĻóGÓėĘ½ŅĘŗóµÄĻ߶ĪÓŠ¹«¹²µćŹ±,nµÄȔֵ·¶Ī§.
”¾“š°ø”æ(1) x=3,a=![]() (2) y=
(2) y=![]() x2-3x(3)n=1»ņ2”Ün”Ü4,
x2-3x(3)n=1»ņ2”Ün”Ü4,
”¾½āĪö”æ
(1)æɵƶž“ĪŗÆŹżx=3£¬æÉĒóµĆaµÄÖµ£»
£Ø2£©ĻČĒó³ö½»µćĪŖ(2,-4)£¬“śČė£Ø1£©½āĪöŹ½æɵƶž“ĪŗÆŹżµÄ½āĪöŹ½£»
(3)æÉĻČĒóµĆA”¢Bµć×ų±ź¼°Ö±Ļßy=-2x-4ĻņÓŅĘ½ŅĘn(n>0)øöµ„Ī»µÄ±ķ“ļŹ½£¬¶ž“ĪŗÆŹżŌŚ2”Üx”Ü7µÄ²æ·ÖĻņ×óĘ½ŅĘnøöµ„Ī»ŗóµĆµ½µÄĶ¼Ļó¼ĒĪŖG£¬æɵĆGµÄŗÆŹż±ķ“ļŹ½£¬Į½ÕßĮŖĮ¢µÄ·½³ĢÓŠ½ā£¬æɵĆnµÄȔֵ·¶Ī§.
(1)”߶ž“ĪŗÆŹżŌŚx=0ŗĶx=6Ź±ŗÆŹżÖµĻąµČ,
”ąøƶž“ĪŗÆŹżµÄ¶Ō³ĘÖįĪŖx=3
”ąx=![]() ,
,
½ā²¢¼ģŃéµĆ:a=![]() .
.
(2)”ßÖ±Ļßy=-2x¹żµć(2,m),
”ąm=-2”Į2=-4,
ÓÉĢāŅā,µć(2,-4)ŌŚÅ×ĪļĻßÉĻ,
ĒŅÓÉ(1)a=![]() ,Å×ĪļĻßĪŖy=
,Å×ĪļĻßĪŖy=![]() x2-3x+b,
x2-3x+b,
æɵĆ:2-6+b=-4,
½āµĆb=0,
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=![]() x2-3x.
x2-3x.
(3)¢ŁČēĶ¼£ŗ
µ±n=1Ź±£¬Ņ»“ĪŗÆŹżĪŖ![]() (-1”Üx”Ü1),GĪŖ
(-1”Üx”Ü1),GĪŖ![]() (1”Üx”Ü6)£¬ÓŠ¹«¹²½»µć£Ø1£¬-4£©£¬¹Źn=1Āś×ćĢõ¼ž;
(1”Üx”Ü6)£¬ÓŠ¹«¹²½»µć£Ø1£¬-4£©£¬¹Źn=1Āś×ćĢõ¼ž;
¢Ś
µ±n=2Ź±, ![]() (0”Üx”Ü2), GĪŖ
(0”Üx”Ü2), GĪŖ![]() (0”Üx”Ü5), ÓŠ¹«¹²½»µć£Ø2£¬-4£©£¬¹Źn=2Āś×ćĢõ¼ž
(0”Üx”Ü5), ÓŠ¹«¹²½»µć£Ø2£¬-4£©£¬¹Źn=2Āś×ćĢõ¼ž
¢Ū
µ±n=4Ź±, ![]() (2”Üx”Ü4), GĪŖ
(2”Üx”Ü4), GĪŖ![]() (-2”Üx”Ü3),“ĖŹ±ÓŠ¹«¹²µć£Ø2£¬0£©
(-2”Üx”Ü3),“ĖŹ±ÓŠ¹«¹²µć£Ø2£¬0£©
¹Ź£ŗn=1»ņ2”Ün”Ü4,


 µŚ1¾ķµ„ŌŖŌĀæ¼ĘŚÖŠĘŚÄ©ĻµĮŠ“š°ø
µŚ1¾ķµ„ŌŖŌĀæ¼ĘŚÖŠĘŚÄ©ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬PDĒŠ”ŃOÓŚµćC£¬ÓėBAµÄŃÓ³¤Ļß½»ÓŚµćD£¬DE”ĶPO½»POŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓPB£¬”ĻEDB=”ĻEPB£®

£Ø1£©ĒóÖ¤£ŗPBŹĒµÄĒŠĻߣ®
£Ø2£©ČōPB=6£¬DB=8£¬Ēó”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
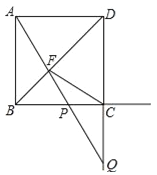
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDµÄ±ß³¤ĪŖ1£¬µćPŌŚÉäĻßBCÉĻ£ØŅģÓŚµćB”¢C£©£¬Ö±ĻßAPÓė¶Ō½ĒĻßBD¼°ÉäĻßDC·Ö±š½»ÓŚµćF”¢Q£®
£Ø1£©ČōBP=![]() £¬Ēó”ĻBAPµÄ¶ČŹż£»
£¬Ēó”ĻBAPµÄ¶ČŹż£»
£Ø2£©ČōµćPŌŚĻ߶ĪBCÉĻ£¬¹żµćF×÷FG”ĶCD£¬“¹×ćĪŖG£¬µ±”÷FGC”Õ”÷QCPŹ±£¬ĒóPCµÄ³¤£»
£Ø3£©ŅŌPQĪŖÖ±¾¶×÷”ŃM£®
¢ŁÅŠ¶ĻFCŗĶ”ŃMµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
¢Śµ±Ö±ĻßBDÓė”ŃMĻąĒŠŹ±£¬Ö±½ÓŠ“³öPCµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() £ŗ
£ŗ![]() £Ø
£Ø![]() £©Óė
£©Óė![]() £¬
£¬![]() Öį·Ö±š½»ÓŚ
Öį·Ö±š½»ÓŚ![]() £¬
£¬![]() Į½µć£¬ŅŌ
Į½µć£¬ŅŌ![]() ĪŖ±ßŌŚÖ±Ļß
ĪŖ±ßŌŚÖ±Ļß![]() µÄÉĻ·½×÷Õż·½ŠĪ
µÄÉĻ·½×÷Õż·½ŠĪ![]() £¬·“±ČĄżŗÆŹż
£¬·“±ČĄżŗÆŹż![]() ŗĶ
ŗĶ![]() µÄĶ¼Ļó·Ö±š¹żµć
µÄĶ¼Ļó·Ö±š¹żµć![]() ŗĶµć
ŗĶµć![]() .Čō
.Čō![]() £¬Ōņ
£¬Ōņ![]() µÄÖµĪŖ______.
µÄÖµĪŖ______.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
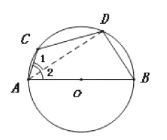
”¾ĢāÄæ”æČēĶ¼,ABŹĒ”Ń0µÄÖ±¾¶,µćCŌŚ”Ń0ÉĻ,DŹĒ![]() ÖŠµć,Čō”ĻBAC=70”ć,Ēó”ĻC.
ÖŠµć,Čō”ĻBAC=70”ć,Ēó”ĻC.
ĻĀĆęŹĒŠ”ö©µÄ½ā·Ø,Ēė°ļĖū²¹³äĶźÕū:
½ā:ŌŚ”Ń0ÖŠ,
”ßDŹĒ![]() µÄÖŠµć
µÄÖŠµć
”ąBD=CD.
”ą”Ļ1=”Ļ2( )(ĢīĶĘĄķµÄŅĄ¾Ż).
”ß”ĻBAC=70”ć,
”ą”Ļ2=35”ć.
”ßABŹĒ”Ń0µÄÖ±¾¶,
”ą”ĻADB=90”ć( )(ĢīĶĘĄķµÄŅĄ¾Ż).
”ą”ĻB=90”ć-”Ļ2=55”ć.
”ßA”¢B”¢C”¢DĖÄøöµć¶¼ŌŚ”Ń0ÉĻ,
”ą”ĻC+”ĻB=180”ć( )(ĢīĶĘĄķµÄŅĄ¾Ż).
”ą”ĻC=180”ć-”ĻB= (Ģī¼ĘĖć½į¹ū).
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĄīÄž×¼±øĶź³ÉĢāÄ棻½ā¶žŌŖŅ»“Ī·½³Ģ×é![]() £¬·¢ĻÖĻµŹż”°”õ”±Ó”Ė¢²»Ē峞£®
£¬·¢ĻÖĻµŹż”°”õ”±Ó”Ė¢²»Ē峞£®
£Ø1£©Ėū°Ń”°”õ”±²Ā³É3£¬ĒėÄć½ā¶žŌŖŅ»“Ī·½³Ģ×é![]() £»
£»
£Ø2£©ÕÅĄĻŹ¦Ėµ£ŗ”°Äć²Ā“ķĮĖ”±£¬ĪŅ擵½øĆĢā±ź×¼“š°øµÄ½į¹ūx”¢yŹĒŅ»¶ŌĻą·“Źż£¬Ķعż¼ĘĖćĖµĆ÷ŌĢāÖŠ”°”õ”±ŹĒ¼ø£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖA£Ø2£¬y1£©£¬B£Ø©3£¬y2£©£¬C£Ø©5£¬y3£©Čżøöµć¶¼ŌŚ·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóÉĻ£¬±Č½Ļy1£¬y2£¬y3µÄ“󊔣¬ŌņĻĀĮŠø÷Ź½ÕżČ·µÄŹĒ£Ø””””£©
µÄĶ¼ĻóÉĻ£¬±Č½Ļy1£¬y2£¬y3µÄ“󊔣¬ŌņĻĀĮŠø÷Ź½ÕżČ·µÄŹĒ£Ø””””£©
A.y1£¼y2£¼y3B.y2£¼y3£¼y1C.y1£¼y3£¼y2D.y3£¼y2£¼y1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
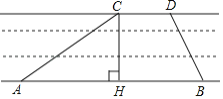
”¾ĢāÄæ”澩ŗ¼“óŌĖŗÓŹĒŹĄ½ēĪÄ»ÆŅŲś£®×ŪŗĻŹµ¼ł»ī¶ÆŠ”×éĪŖĮĖ²ā³öij¶ĪŌĖŗÓµÄŗÓæķ£Ø°¶ŃŲŹĒĘ½ŠŠµÄ£©£¬ČēĶ¼£¬ŌŚ°¶±ß·Ö±šŃ”¶ØĮĖµćA”¢BŗĶµćC”¢D£¬ĻČÓĆ¾ķ³ßĮæµĆAB=160m£¬CD=40m£¬ŌŁÓĆ²ā½ĒŅĒ²āµĆ”ĻCAB=30”ć£¬”ĻDBA=60”ć£¬ĒóøƶĪŌĖŗÓµÄŗÓæķ£Ø¼“CHµÄ³¤£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”ææ×Ć÷Ķ¬Ń§¶Ō±¾Š£Ń§Éś»į×éÖƵĔ°ĪŖʶĄ§É½ĒųĻ×°®ŠÄ”±×ŌŌø¾čæī»ī¶Æ½ųŠŠ³éŃłµ÷²é£¬µĆµ½ĮĖŅ»×éѧɜ¾čæīĒéæöµÄŹż¾Ż£®ČēĶ¼ŹĒøł¾ŻÕā×鏿¾Ż»ęÖʵÄĶ³¼ĘĶ¼£¬Ķ¼ÖŠ“Ó×óµ½ÓŅø÷³¤·½ŠĪµÄø߶ČÖ®±ČĪŖ3£ŗ4£ŗ5£ŗ10£ŗ8£¬ÓÖÖŖ“Ė“Īµ÷²éÖŠ¾čæī30ŌŖµÄѧɜŅ»¹²16ČĖ£®
£Ø1£©æ×Ć÷Ķ¬Ń§µ÷²éµÄÕā×éѧɜ¹²ÓŠ_______ČĖ£»
£Ø2£©Õā×鏿¾ŻµÄÖŚŹżŹĒ_____ŌŖ£¬ÖŠĪ»ŹżŹĒ_____ŌŖ£»
£Ø3£©ČōøĆŠ£ÓŠ2000Ćūѧɜ£¬¶¼½ųŠŠĮĖ¾čæī£¬¹Ą¼ĘČ«Š£Ń§Éś¹²¾čæī¶ąÉŁŌŖ£æ

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com