
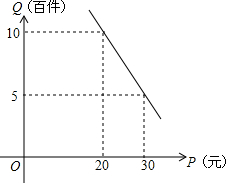
 在精准对口扶贫活动中,甲单位将经营状况良好的某种专卖店以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的乙户,并约定从该店经营的利润中,首先保证乙户的一家人每月最低生活费的开支3600元后,逐步偿还转让费(不计利息).从甲单位提供的相关资料中可知这种消费品的进价是每件14元;月销售量Q(百件)与销售单价P(元)的关系如图所示;维持的正常运转每月需工资外的各种开支2000元.
在精准对口扶贫活动中,甲单位将经营状况良好的某种专卖店以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的乙户,并约定从该店经营的利润中,首先保证乙户的一家人每月最低生活费的开支3600元后,逐步偿还转让费(不计利息).从甲单位提供的相关资料中可知这种消费品的进价是每件14元;月销售量Q(百件)与销售单价P(元)的关系如图所示;维持的正常运转每月需工资外的各种开支2000元.分析 (1)代入点(20,10)(30,5)即可求得Q与P的函数关系式;
(2)月利润为W,可得出W关于P的二次函数,即可解题;
(3)根据(2)中结论,根据每月都是最大利润时脱贫需要月份即可解题.
解答 (1)由图象可知,月销售量Q(百件)与销售单价P(元)是一次函数关系,设Q=Px+b,
则代入(20,10)(30,5),可得$\left\{\begin{array}{l}{10=20P+b}\\{5=30P+b}\end{array}\right.$,
解得:P=-$\frac{1}{2}$,b=20,
∴月销售量Q(百件)与销售单价P(元)的函数关系式为Q=-$\frac{1}{2}$P+20;
(2)设月利润为W,则有W=100 Q(P-14)-(2000+3600)
=100(-$\frac{1}{2}$P+20)(x-14)-(2000+3600)
=-50P2+2700P-33600,
当P=-$\frac{2700}{2×(-50)}$=27时,W有最大值;
∴当销售单价为27元时,月利润余额最大;
(3)设x 年内可脱贫,由(2)知当P=27时,W有最大值为2850,
当月利润为2850元时,需要2850×12x≥50000+58000,
解得:x≥3.2,
∴乙户依靠该店,最早可望在3.2年内脱贫.
点评 本题考查了二次函数的性质在实际生活中的应用.最大月利润的问题常利用二次函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
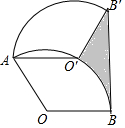 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$ | B. | 2$\sqrt{3}$-$\frac{π}{3}$ | C. | 2$\sqrt{3}$-$\frac{2π}{3}$ | D. | 4$\sqrt{3}$-$\frac{2π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
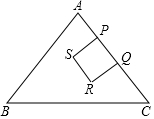 如图,在△ABC中,AB=AC=5,BC=6,P、Q两点同时从点A出发,点P沿AC边运动,速度为每秒1个单位:点Q沿A→C→B运动,速度为每秒2个单位,以PQ为边,在PQ左侧作正方形PQRS(P、Q、R、S按顺时针方向标记).设点P的运动时间为t(秒),正方形PQRS与△ABC的重叠部分的面积为S(平方单位).
如图,在△ABC中,AB=AC=5,BC=6,P、Q两点同时从点A出发,点P沿AC边运动,速度为每秒1个单位:点Q沿A→C→B运动,速度为每秒2个单位,以PQ为边,在PQ左侧作正方形PQRS(P、Q、R、S按顺时针方向标记).设点P的运动时间为t(秒),正方形PQRS与△ABC的重叠部分的面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com