

���� ��1�����������ε������ʽֱ�ӵó����ۣ����ȵ�ͬ�ߵ����������������ȣ���
��2�����ã�1���Ľ��ۣ��ó�S��ABD=$\frac{1}{2}$S��ABC��S��BCE=$\frac{1}{2}$S��ABC������������ĺͣ����ɣ�
��3�����ã�1���Ľ��ۣ��ó�S��CBD=S��ABC��S��CBD=S��CED����������ĺ�S��BDE=2S��ABC��S��ADF=2S��ABC��S��CEF=2S��ABC�����ɣ�
��4��ͬ��3���ķ������ɵ�֤��
��� �⣺��1����ͼ1��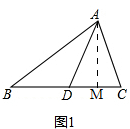 ����A��AM��BC��
����A��AM��BC��
��AD�ǡ�ABC�����ߣ�
��BD=CD=$\frac{1}{2}$BC��
��S��ABD=$\frac{1}{2}$BD��AM��S��ACD=$\frac{1}{2}$CD��AM
��S��ABD=S��ACD��
��2��S��ABF=S�ı���CDFE��
���ɣ���ͼ1����AD�ǡ�ABC�����ߣ�
��BD=CD=$\frac{1}{2}$BC��
��S��ABD=$\frac{1}{2}$BD��AM��S��ABC=$\frac{1}{2}$BC��AM
��S��ABD=$\frac{1}{2}$S��ABC��
��ͬ����S��BCE=$\frac{1}{2}$S��ABC��
��S��ABD=S��BCE��
��S��ABF+S��DBF=S�ı���CDFE+S��BDF��
��S��ABF=S�ı���CDFE��
��3����ͼ3��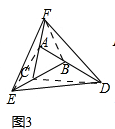
����BF��AE��CD
�ߡ�ABC�ĸ��߰�˳ʱ�뷽���ӳ�һ����
��BD=AB��CE=BC��AF=AC��
�ã�1�����ۣ�
�ڡ�ACD�У�S��CBD=S��ABC��
�ڡ�BDE�У�S��CBD=S��CED��
��S��BDE=2S��ABC��
ͬ����S��ADF=2S��ABC��
S��CEF=2S��ABC��
��S��DEF=S��BDE+S��ADF+S��CEF+S��ABC=2S��ABC+2S��ABC+2S��ABC+S��ABC=7S��ABC��
��4��S�ı���A'B'C'D'=5S�ı���ABCD��
���ɣ���ͼ4��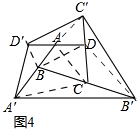
���ӣ�AC'��BD'��A'C��B'D��BD��
�߽��ı���ABCD���߰���ʱ�뷽����ӳ�һ�����õ��ı���A'B'C'D'��
��BC=B'C��CD=C'D��AD=AD'AB=A'B��
�ã�1���Ľ��ۣ�ͬ��2����������
S��B'CC'=2S��BCD��
S��C'DD'=2S��ACD��
S��A'BB'=2S��ABD��
S��A'BB'=2S��ABC��
��S�ı���A'B'C'D'=S��B'CC'+S��C'DD'+S��A'BB'+S��A'BB'+S�ı���ABCD
=2S��BCD+2S��ACD+2S��ABD+2S��ABC+S�ı���ABCD
=2��S��BCD+S��ACD+S��ABD+S��ABC��+S�ı���ABCD
=2��2S�ı���ABCD+S�ı���ABCD
=5S�ı���ABCD��
���� �����������ε��ۺ��⣬��Ҫ�����������ε�����������ε����߷ֵ����������ε������ԭ����İ룬�Ȿ��Ĺؼ����жϳ�S��ABD=$\frac{1}{2}$S��ABC��


 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 2 | C�� | 3 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��5 | B�� | a��5 | C�� | a��5 | D�� | a��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC�ߵ��е㣬��DE=2����BC�ij����ǣ�������
��ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC�ߵ��е㣬��DE=2����BC�ij����ǣ�������| A�� | 6 | B�� | 5 | C�� | 4 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����C���߶�BD�ϣ�AB��BD��PD��BD����B=��D=90�㣬AB=3��BC=6��CD=2����DE=1��4ʱ����ABC���CDE���ƣ�
��ͼ����C���߶�BD�ϣ�AB��BD��PD��BD����B=��D=90�㣬AB=3��BC=6��CD=2����DE=1��4ʱ����ABC���CDE���ƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=x2-��k+2��x+$\frac{5k+2}{4}$��ֱ��y=��k+1��x+��k+1��2��
��֪������y=x2-��k+2��x+$\frac{5k+2}{4}$��ֱ��y=��k+1��x+��k+1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com