
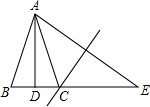
 如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:| A. | 只有① | B. | 只有①② | C. | 只有①②③ | D. | 只有①④ |
分析 由线段垂直平分线的性质可得CA=CE,又可判定AB=AC,可得AB+BD=AC+CD=CE+CD=DE,由于∠E≠30°,于是得到AD≠$\frac{1}{2}$AE,由BD=CD<AC,故④错误.
解答 解:∵BD=CD,AD⊥BC,
∴AD为BC的垂直平分线,
∴AB=AC,
又C在AE的垂直平分线上,
∴AC=CE,
∴AB=AC=CE,故①正确,
∴AB+BD=AC+CD=CE+CD=DE,故②正确,
∵∠E≠30°,
∴AD≠$\frac{1}{2}$AE,故③错误,
∵BD=CD<AC,故④错误.
故选B.
点评 本题主要考查线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
 如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题:
如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| ①始发站 | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩终点站 | |
| 上客人数 | 9 | 8 | 10 | 12 | 14 | 13 | 11 | 6 | 7 | 0 |
| 下客人数 | 0 | -3 | -5 | -7 | -4 | -8 | -6 | -9 | x | -28 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com