
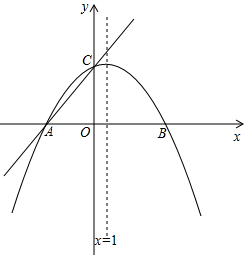
 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=$\frac{5}{4}$x+m��mΪ��������ͼ����x�ύ�ڵ�A��-3��0������y�ύ�ڵ�C����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=$\frac{5}{4}$x+m��mΪ��������ͼ����x�ύ�ڵ�A��-3��0������y�ύ�ڵ�C����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B���� ��1����A��-3��0������y=$\frac{5}{4}$x+m���������m��ֵ���õ�һ�κ����Ľ���ʽ�������C�����꣮����������y=ax2+bx+c�ĶԳ�����ֱ��x=1���Ҿ���A��C���г�����a��b��c�ķ����飬�ⷽ���鼴����������ߵĺ�������ʽ��
��2����Q��x��-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$���������ACQ����ACΪֱ�DZߵ�ֱ��������ʱ��������������ٵ�CΪֱ�Ƕ���ʱ����CQ��AC���������ڵ�Q��QE��y����E��֤����ACO�ס�CQE���������������ζ�Ӧ�߳ɱ������x��ֵ���ڵ�AΪֱ�Ƕ���ʱ����AQ���AC���������ڵ�Q�䣬Q��E���x����E��֤����ACO�ס�Q��AE�䣬�������������ζ�Ӧ�߳ɱ������x��ֵ��
��3����ACP�ܳ���Сʱ��PΪֱ��BC��Գ���Ľ��㣮���ݶ��κ����ĶԳ������B�����꣬���ô���ϵ�������ֱ��BC�Ľ���ʽ����x=1���룬���P������Ϊ��1��3���������P��ֱ��Ϊ��y=kx+3-k����y=kx+3-k����y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$�������õ�x2+��4k-2��x-4k-3=0�����ø���ϵ���Ĺ�ϵ�ó�x1+x2=2-4k��x1x2=-4k-3����y1-y2=k��x1-x2����Ȼ����������ľ��빫ʽ���M1M2=${\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}}^{\;}$=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}-{x}_{2}��^{2}}$=4��1+k2����M1P=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}-1��^{2}}$��M2P=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{2}-1��^{2}}$����ôM1P•M2P=4��1+k2���������ó�$\frac{{M}_{1}P•{M}_{2}P}{{M}_{1}{M}_{2}}$=1Ϊ��ֵ��
��� �⣺��1����һ�κ���y=$\frac{5}{4}$x+m��mΪ��������ͼ����x�ύ�ڵ�A��-3��0����
��0=$\frac{5}{4}$����-3��+m�����m=$\frac{15}{4}$��
��һ�κ�������ʽΪy=$\frac{5}{4}$x+$\frac{15}{4}$��
��C��������0��$\frac{15}{4}$����
����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��-3��0����C��0��$\frac{15}{4}$����
��$\left\{\begin{array}{l}{-\frac{b}{2a}=1}\\{9a-3b+c=0}\\{c=\frac{15}{4}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{1}{2}}\\{c=\frac{15}{4}}\end{array}\right.$��
�������ߵĺ�������ʽΪy=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$��
��2�����ڣ���Q��x��-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$����
�ٵ���CΪֱ�Ƕ���ʱ����ͼ����CQ��AC���������ڵ�Q��QE��y����E��
�ڡ�ACO���CQE�У�
$\left\{\begin{array}{l}{��ACO=��CQE=90��-��QCE}\\{��AOC=��CEQ}\end{array}\right.$��
���ACO�ס�CQE��
��$\frac{QE}{CO}$=$\frac{CE}{AO}$����$\frac{x}{\frac{15}{4}}$=$\frac{\frac{15}{4}-��-\frac{1}{4}{x}^{2}+\frac{1}{2}x+\frac{15}{4}��}{3}$��
���x1=5.2��x2=0������������ȥ����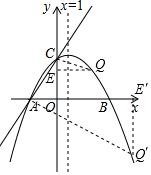 �ڵ���AΪֱ�Ƕ���ʱ����ͼ����AQ���AC���������ڵ�Q�䣬Q��E���x����E��
�ڵ���AΪֱ�Ƕ���ʱ����ͼ����AQ���AC���������ڵ�Q�䣬Q��E���x����E��
�ڡ�ACO���Q��AE���У�
$\left\{\begin{array}{l}{��OAC=��E��Q��A=90��-��OAQ��}\\{��AOC=��Q��E��A}\end{array}\right.$��
���ACO�ס�Q��AE�䣬
��$\frac{AE��}{CO}$=$\frac{Q��E��}{AO}$����$\frac{x+3}{\frac{15}{4}}$=$\frac{\frac{1}{4}{x}^{2}-\frac{1}{2}x-\frac{15}{4}}{3}$��
���x1=8.2��x2=-3������������ȥ����
����������Q��ĺ�����Ϊ5.2��8.2��
��3����y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$��x�ύ��A��-3��0����B���㣬�Գ���Ϊֱ��x=1��
��B��������5��0����
��C��0��$\frac{15}{4}$����
��ֱ��BC�Ľ���ʽΪy=-$\frac{3}{4}$x+$\frac{15}{4}$��
��x=1ʱ��y=-$\frac{3}{4}$��1+$\frac{15}{4}$=3��
��P��1��3����
�����P��ֱ��Ϊ��y=kx+3-k��
��y=kx+3-k����y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$��
��kx+3-k=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{15}{4}$��
�����ã�x2+��4k-2��x-4k-3=0��
��x1+x2=2-4k��x1x2=-4k-3��y1-y2=k��x1-x2����
�ࣨx1-x2��2=��x1+x2��2-4x1x2=��2-4k��2-4��-4k-3��=16k2+16��
��M1M2=${\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}}^{\;}$=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}-{x}_{2}��^{2}}$=4��1+k2����
ͬ����M1P=$\sqrt{��{x}_{1}-1��^{2}+��k{x}_{1}+3-k-3��^{2}}$=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}-1��^{2}}$��
M2P=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{2}-1��^{2}}$��
��M1P•M2P=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}-1��^{2}}$•$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{2}-1��^{2}}$=|��x1-1����x2-1��|•��1+k2��=4��1+k2����
��$\frac{{M}_{1}P•{M}_{2}P}{{M}_{1}{M}_{2}}$=1Ϊ��ֵ��
���� �����Ƕ��κ����ۺ��⣬�����漰�����ô���ϵ�����������ߡ�ֱ�ߵĽ���ʽ�����κ��������ʣ����������ε��ж������ʣ���Գ�-���·�����⣬����ϵ���Ĺ�ϵ�������ľ��빫ʽ��֪ʶ���ۺ��Խ�ǿ���Ѷ����У����Ǽ������ϴ����÷���˼�롢���ν������������ǽ���Ĺؼ���


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������ξֵ������ԡ���һ���ڼ�������ε�����̶� | |
| B�� | �����й����ڶ������ں���������ϵͳ�ַ���̬�ȵı��� | |
| C�� | �����й�������ĸ���㲿�������� | |
| D�� | ���������г�2017��ѧ�����п��忼�ɼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
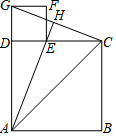 ��ͼ����֪�ı���ABCD���ı���DEFGΪ�����Σ���E���߶�DC�ϣ���A��D��G��ͬһֱ���ϣ���AD=3��DE=1������AC��CG��AE�����ӳ�AE��OG�ڵ�H��
��ͼ����֪�ı���ABCD���ı���DEFGΪ�����Σ���E���߶�DC�ϣ���A��D��G��ͬһֱ���ϣ���AD=3��DE=1������AC��CG��AE�����ӳ�AE��OG�ڵ�H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����1��
����1��| �����ϵ�� ���ڻ����60% | �����ϵ�� ��50%��60%֮�� | �����ϵ�� ��40%��50%֮�� | �����ϵ�� ��30%��40%֮�� | �����ϵ�� С��30% |
| ����ƶ�� | �� �� | С �� | �� ԣ | �ԣ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com