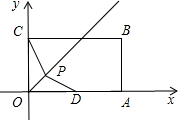
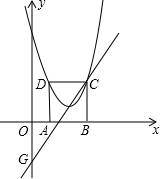
ЃЈ1ЃЉЁпЕуDЪЧOAЕФжаЕуЃЌ
ЁрOD=2ЃЌ
ЁрOD=OCЃЎ
гжЁпOPЪЧЁЯCODЕФНЧЦНЗжЯпЃЌ
ЁрЁЯPOC=ЁЯPOD=45ЁуЃЌ
ЁрЁїPOCЁеЁїPODЃЌ
ЁрPC=PDЃЎ
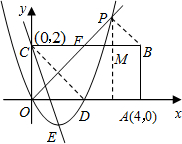
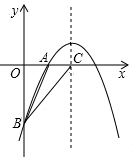
ЃЈ2ЃЉЙ§ЕуBзїЁЯAOCЕФЦНЗжЯпЕФДЙЯпЃЌДЙзуЮЊPЃЌЕуPМДЮЊЫљЧѓЃЎ
взжЊЕуFЕФзјБъЮЊЃЈ2ЃЌ2ЃЉЃЌЙЪBF=2ЃЌзїPMЁЭBFЃЌ
ЁпЁїPBFЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPM=
BF=1ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ3ЃЌ3ЃЉЃЎ
ЁпХзЮяЯпОЙ§дЕуЃЌ
ЁрЩшХзЮяЯпЕФНтЮіЪНЮЊy=ax
2+bxЃЎ
гжЁпХзЮяЯпОЙ§ЕуPЃЈ3ЃЌ3ЃЉКЭЕуDЃЈ2ЃЌ0ЃЉЃЌ
Ёрга
НтЕУ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=x
2-2xЃЛ
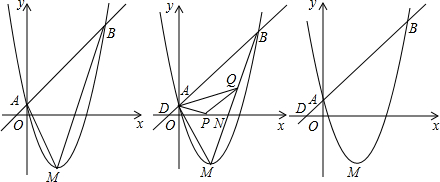
ЃЈ3ЃЉгЩЕШбќжБНЧШ§НЧаЮЕФЖдГЦаджЊDЕуЙигкЁЯAOCЕФЦНЗжЯпЕФЖдГЦЕуМДЮЊCЕуЃЎ
СЌНгECЃЌЫќгыЁЯAOCЕФЦНЗжЯпЕФНЛЕуМДЮЊЫљЧѓЕФPЕуЃЈвђЮЊPE+PD=ECЃЌЖјСНЕужЎМфЯпЖЮзюЖЬЃЉЃЌДЫЪБЁїPEDЕФжмГЄзюаЁЃЎ
ЁпХзЮяЯпy=x
2-2xЕФЖЅЕуEЕФзјБъЃЈ1ЃЌ-1ЃЉЃЌCЕуЕФзјБъЃЈ0ЃЌ2ЃЉЃЌ
ЩшCEЫљдкжБЯпЕФНтЮіЪНЮЊy=kx+bЃЌ
дђга
ЃЌ
НтЕУ
ЃЎ
ЁрCEЫљдкжБЯпЕФНтЮіЪНЮЊy=-3x+2ЃЎ
ЕуPТњзу
ЃЌ
НтЕУ
ЃЌ
ЙЪЕуPЕФзјБъЮЊ
(ЃЌ)ЃЎ
ЁїPEDЕФжмГЄМДЪЧCE+DE=
+
ЃЛ
ЃЈ4ЃЉМйЩшДцдкЗћКЯЬѕМўЕФPЕуЃЎОиаЮЕФЖдГЦжааФЮЊЖдНЧЯпЕФНЛЕуЃЌЙЪNЃЈ2ЃЌ1ЃЉЃЎ
ЂйЕБPЕудкNЕуЩЯЗНЪБЃЌгЩЃЈ2ЃЉжЊFЃЈ2ЃЌ2ЃЉЃЌЧвЁЯNFC=90ЁуЃЌЯдШЛFЕуЗћКЯPЕуЕФвЊЧѓЃЌЙЪPЃЈ2ЃЌ2ЃЉЃЛ
ЂкЕБPЕудкNЕуЯТЗНЪБЃЌЩшPЃЈaЃЌaЃЉЃЌдђЃКЁпCЃЈ0ЃЌ2ЃЉЃЌNЃЈ2ЃЌ1ЃЉЃЌЁргЩЙДЙЩЖЈРэЕУЃЌCP
2+PN
2=CN
2ЃЌМДa
2+ЃЈa-2ЃЉ
2+ЃЈ2-aЃЉ
2+ЃЈ1-aЃЉ
2=5ЃЌМД4a
2-10a+4=0ЃЌНтЕУa=
Лђa=2ЃЌЙЪPЃЈ
ЃЌ
ЃЉЃЌ
злЩЯПЩжЊЃКДцдкЕуPЃЌЪЙЁЯCPN=90ЖШЃЎЦфзјБъЪЧ
(ЃЌ)ЛђЃЈ2ЃЌ2ЃЉЃЎ

 ЦНЗжЯпЩЯЕФвЛИіЖЏЕуЃЈВЛгыЕуOжиКЯЃЉЃЎ
ЦНЗжЯпЩЯЕФвЛИіЖЏЕуЃЈВЛгыЕуOжиКЯЃЉЃЎ


 AМгН№Ьт ЯЕСаД№АИ
AМгН№Ьт ЯЕСаД№АИ ШЋгХВтЪдОэЯЕСаД№АИ
ШЋгХВтЪдОэЯЕСаД№АИ

 зюДѓжЕЮЊЖрЩйЃП
зюДѓжЕЮЊЖрЩйЃП