
分析 (1)原式利用算术平方根,零指数幂、负整数指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原式=5+9-1-$\sqrt{3}$+$\sqrt{3}$=13;
(2)原式=-$\frac{4x}{(x+3)(x-3)}$÷$\frac{3{x}^{2}+9x-{x}^{2}+3x}{(x+3)(x-3)}$=-$\frac{4x}{(x+3)(x-3)}$•$\frac{(x+3)(x-3)}{2x(x+6)}$=-$\frac{2}{x+6}$,
当x=$\sqrt{2}$-6时,原式=-$\frac{2}{\sqrt{2}-6+6}$=-$\frac{2}{\sqrt{2}}$=-$\sqrt{2}$.
点评 此题考查了实数的运算,以及分式的化简求值,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求:
如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
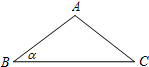 如图,底角为α的等腰△ABC绕着点B顺时针旋转,使得点A与边BC上的点D重合,点C与点E重合,联结AD、CE.已知tanα=$\frac{3}{4}$,AB=5,则CE=$\frac{8\sqrt{10}}{5}$.
如图,底角为α的等腰△ABC绕着点B顺时针旋转,使得点A与边BC上的点D重合,点C与点E重合,联结AD、CE.已知tanα=$\frac{3}{4}$,AB=5,则CE=$\frac{8\sqrt{10}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com