
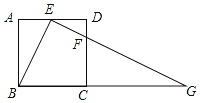
【题目】如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=![]() DC,连结EF并延长交BC的延长线于点G,连结BE.
DC,连结EF并延长交BC的延长线于点G,连结BE.
(1)求证:△ABE∽△DEF.
(2)若正方形的边长为4,求BG的长.
【答案】(1)见解析;(2)BG=BC+CG=10.
【解析】
(1)利用正方形的性质,可得∠A=∠D,根据已知可得AE:AB=DF:DE,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
(2)根据相似三角形的预备定理得到△EDF∽△GCF,再根据相似的性质即可求得CG的长,那么BG的长也就不难得到.
(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90 °.
∵AE=ED,
∴AE:AB=1:2.
∵DF=![]() DC,
DC,
∴DF:DE=1:2,
∴AE:AB=DF:DE,
∴△ABE∽△DEF;
(2)解:∵ABCD为正方形,
∴ED∥BG,
∴△EDF∽△GCF,
∴ED:CG=DF:CF.
又∵DF=![]() DC,正方形的边长为4,
DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
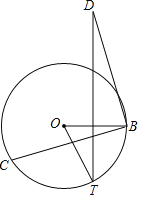
【题目】如图,C为圆O上一动点(不与点B重合),点T为圆O上一动点,且∠BOT=60°,将BC绕点B顺时针旋转90°得到BD,连接TD,当TD最大时,∠BDT的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别标有数字![]() 、
、![]() 、
、![]() 的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为
的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为![]() (不放回),再从中任意抽取一张,将上面的数字记为
(不放回),再从中任意抽取一张,将上面的数字记为![]() ,这样的数字
,这样的数字![]() ,
,![]() 能使关于
能使关于![]() 的一元二次方程
的一元二次方程![]() 有两个正根的概率为________.
有两个正根的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:如图,AD为⊙O的直径。
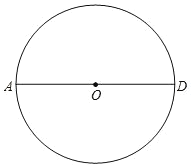
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
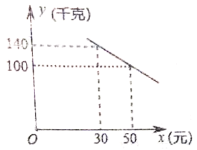
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
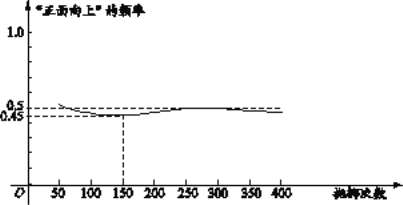
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两个不透明的盒子,
两个不透明的盒子,![]() 盒中装有红色、黄色、蓝色卡片各1张,
盒中装有红色、黄色、蓝色卡片各1张,![]() 盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从
盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从![]() 、
、![]() 两个盒子中任意摸出一张卡片.
两个盒子中任意摸出一张卡片.
(1)从![]() 盒中摸出红色卡片的概率为______;
盒中摸出红色卡片的概率为______;
(2)用画树状图或列表的方法,求摸出的两张卡片中至少有一张红色卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
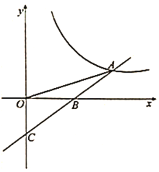
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com