
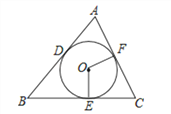
【题目】如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
【答案】(1)2cm;(2)![]() cm2;(3)(
cm2;(3)(![]() +4)cm.
+4)cm.
【解析】试题分析:(1)连接AO、BO、CO,根据S△ABC=S△AOC+S△AOB+S△BOC即可求出⊙O的半径;
(2)因为OF⊥AC,OE⊥BC,∠C=60°可求出∠EOF的度数,代入扇形面积计算公式即可求出扇形的面积;
(3)利用扇形的周长=扇形的弧长+半径×2,即可求出扇形的周长.
试题解析:(1)如图,连接AO、BO、CO,
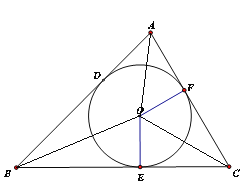
则S△ABC=S△AOC+S△AOB+S△BOC
![]()
![]() ,
,
又AB+BC+AC=10,
∴r=2cm;
(2)因为OF⊥AC,OE⊥BC,∠C=60°
所以∠EOF=120°
所以S扇形EOF=![]() cm2
cm2
(3)扇形EOF的周长=![]() (cm).
(cm).
考点: 1.面积法;2.扇形面积计算;3.扇形弧长计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,矩形内一动点P使得S△PAD=![]() S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.
S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一个基本的几何定理,早在我国西汉吋期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”;这三个整数叫做一组“勾股数”,如:3,4,5;5,12,13;7,24,25;8,15,17;9,40,41等等都是勾股数.
(1)小李在研究勾股数时发现,某些整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差.如3,4,5中,5=22+12,3=22﹣12;5,12,13中,13=32+22,5=32﹣22;请证明:m,n为正整数,且m>n,若有一个直角三角形斜边长为m2+n2,有一条直角长为m2﹣n2,则该直角三角形一定为“整数直角三角形”;
(2)有一个直角三角形两直角边长分别为![]() 和
和![]() ,斜边长4
,斜边长4![]() ,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
(3)若c1=a12+b12,c2=a22+b22,其中,a1、a2、b1、b2均为正整数.证明:存在一个整数直角三角形,其斜边长为c1c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )

A.96B.48C.60D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF.其中正确的结论有( )
S△ABF.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
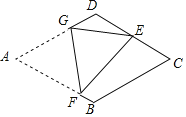
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com