
【题目】如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求![]() 的值;
的值;
(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出![]() 的值.
的值.

【答案】(1)证明见解析; (2)![]() (3)
(3)![]()
【解析】试题分析:(1)只要证明∠ACD=∠BCE,即可根据SAS证得△ACD≌△BCE;
(2)首先证明△ACD∽△BCE,得![]() ,再根据AD=
,再根据AD=![]() BC即可解决问题.
BC即可解决问题.
(3)如图3中,作CH⊥BG于H.设OD=k,则AD=nk,BE=![]() nk,AO=(n+1)k,首先证明△ABC≌△HBC,得BH=CH=AB=AC=
nk,AO=(n+1)k,首先证明△ABC≌△HBC,得BH=CH=AB=AC=![]() (n+1)k,BF=
(n+1)k,BF=![]() nk,求出BG即可解决问题.
nk,求出BG即可解决问题.
试题解析:(1)证明:如图1中,

∵△ABC和△CDE为等边三角形,
∴AC=BC,CD=CE.∠ACB=∠DCE=60°,
∴∠ACB-∠DCO=∠DCE-∠DCO,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS);
(2)如图2中,

∵AB=AC,OA平分∠BAC,
∴AO⊥BC,OB=OC,
∵∠BAC=∠EDC=90°,AB=AC,DE=DC,
∴∠ACB=∠DCE=45°,BC=![]() AC,EC=
AC,EC=![]() CD,
CD,
∴![]() ,∠ACD=∠BCE,
,∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() ,
,
∵OA=OB=OC,AD=OD,
∴AD=![]() BC,
BC,
∴![]() ,
,
∴![]() .
.
(3)如图3中,作CH⊥BG于H.

由(2)可知△ACD∽△BCE,
∴BE:AD=![]() ,∠CAD=∠CBE=45°,设OD=k,则AD=nk,BE=
,∠CAD=∠CBE=45°,设OD=k,则AD=nk,BE=![]() nk,AO=(n+1)k,
nk,AO=(n+1)k,
∵∠ABC=∠HBC=45°,∠BAC=∠BHC,BC=BC,
∴△ABC≌△HBC,
∴BH=CH=AB=AC=![]() (n+1)k,BF=
(n+1)k,BF=![]() nk,
nk,
FH=HG=![]() (n+1)k-
(n+1)k-![]() nk,
nk,
∴ .
.


科目:初中数学 来源: 题型:
【题目】下列说法:
①三角形的三条内角平分线都在三角形内,且相交于一点;
②在![]() 中,若
中,若![]() ,则
,则![]() 一定是直角三角形;
一定是直角三角形;
③三角形的一个外角大于任何一个内角;
④若等腰三角形的两边长分别是3和5,则周长是13或11;
⑤如果一个正多边形的每一个内角都比其外角多![]() ,那么该正多边形的边数是10,
,那么该正多边形的边数是10,
其中正确的说法有________________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一根弹簧的长度为10厘米,当弹簧受到![]() 千克的拉力时(
千克的拉力时(![]() 不超过10),弹簧的长度是
不超过10),弹簧的长度是![]() (厘米),测得有关数据如下表所示:
(厘米),测得有关数据如下表所示:
拉力 | 1 | 2 | 3 | 4 | … |
弹簧的长度 |
|
|
|
| … |
(1)写出弹簧长度![]() (厘米)关于拉力
(厘米)关于拉力![]() (千克)的函数解析式;
(千克)的函数解析式;
(2)如果拉力是10千克,那么弹簧长度是多少厘米?
(3)当拉力是多少时,弹簧长度是14厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
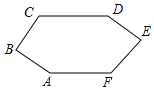
【题目】如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
(1)观察直线AB与直线DE的位置关系,你能得出什么结论并说明理由.
(2)求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )
次数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
频率 | 0.60 | 0.30 | 0.50 | 0.36 | 0.42 | 0.38 | 0.41 | 0.39 | 0.40 | 0.40 |
A. 掷一个质地均匀的骰子,向上的面点数是“6”
B. 掷一枚一元的硬币,正面朝上
C. 不透明的袋子里有2个红球和3个黄球,除颜色外都相同,从中任取一球是红球
D. 三张扑克牌,分别是3,5,5,背面朝上洗匀后,随机抽出一张是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书定价8元,如果一次购买10本以上,超过10本的部分打八折,在这个问题中,当购书的数量变化时,付款金额也随之发生了变化.
(1)如果购书的数量用x(本)表示,付款金额用y(元)表示,求y与x之间的关系式;
(2)当购书20本时,付款金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 两地相距
两地相距![]() ,甲骑自行车,乙骑摩托车沿一条笔直的公路由
,甲骑自行车,乙骑摩托车沿一条笔直的公路由![]() 地匀速行驶到
地匀速行驶到![]() 地.设行驶时间为
地.设行驶时间为![]() ,甲、乙离开
,甲、乙离开![]() 地的路程分别记为
地的路程分别记为![]() ,
,![]() ,它们与
,它们与![]() 的关系如图所示.
的关系如图所示.

(1)分别求出线段![]() ,
,![]() 所在直线的函数表达式.
所在直线的函数表达式.
(2)试求点![]() 的坐标,并说明其实际意义.
的坐标,并说明其实际意义.
(3)乙在行驶过程中,求两人距离超过![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线BC方向平移3 cm得到△DEF.若△ABC的周长为14 cm,则四边形ABFD的周长为( )

A. 20 cmB. 17 cm
C. 14 cmD. 23 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com