
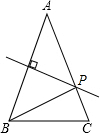
 如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点.
如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点.分析 (1)根据线段垂直平分线上的点到线段两端点的距离相等可得AP=BP,根据等边对等角可得∠A=∠ABP,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)求出△PBC的周长=AB+BC,代入数据计算即可得解.
解答 解:(1)∵AB的垂直平分线交AC于P点,
∴AP=BP,
∴∠A=∠ABP=35°,
∴∠BPC=∠A+∠ABP=35°+35°=70°;
(2)△PBC的周长=BP+PC+BC,
=AP+PC+BC,
=AC+BC,
=AB+BC,
∵AB=5cm,BC=3cm,
∴△PBC的周长=5+3=8cm.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,熟记性质并准确识图是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:选择题
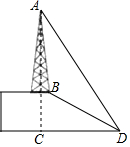 某公司移动电话信号收发塔AB建在学校的科技楼BC上,小飞同学利用测倾器在与点C距离为27米远的点D处测得塔顶A的仰角为60°,塔底B的仰角为30°,则信号收发塔AB的高度约为( )米.(精确到0.1米,$\sqrt{3}≈1.73,\sqrt{5}≈2.24$)
某公司移动电话信号收发塔AB建在学校的科技楼BC上,小飞同学利用测倾器在与点C距离为27米远的点D处测得塔顶A的仰角为60°,塔底B的仰角为30°,则信号收发塔AB的高度约为( )米.(精确到0.1米,$\sqrt{3}≈1.73,\sqrt{5}≈2.24$)| A. | 31.2 | B. | 31.1 | C. | 30.2 | D. | 30.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
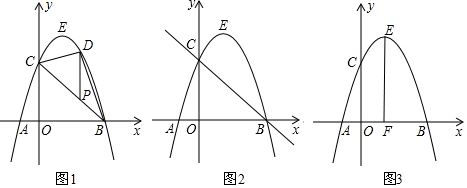
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
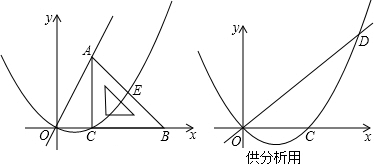
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com