
����Ŀ����ͼ����ʾ����֪�ھ���ABCD�У�AB=60cm��BC=90cm����P�ӵ�A��������3cm/s���ٶ���AB�˶���ͬʱ����Q�ӵ�B��������20cm/s���ٶ���BC�˶�������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P��Q�˶���ʱ��Ϊt��s����
��1����t=sʱ����BPQΪ���������Σ�
��2����BDƽ��PQʱ����t��ֵ��
��3����ͼ�ڣ�����BPQ��PQ�۵�����B�Ķ�Ӧ��ΪE��PE��QE�ֱ���AD���ڵ�F��G��
̽�����Ƿ����ʵ��t��ʹ��AF=EF��������ڣ����t��ֵ����������ڣ�˵�����ɣ�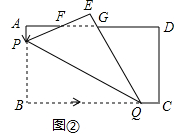
���𰸡�
��1��![]()
��2��
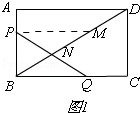
�⣺��ͼ1��
��P��PM��AD��
�� ![]() ��
��
�� ![]() ��
��
��PM=90�� ![]() t��
t��
��PN=NQ��PM=BQ��
��90�� ![]() t=20t��
t=20t��
��t= ![]() ��
��
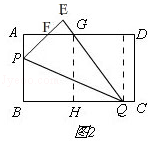
��3��
�⣺��ͼ2����GH��BQ��H��
��PB=PF=60��3t��
��AE=EF����AEP=��FEG����A=��F��
���AEP�ա�FEG��
��PE=EG��FG=AP��
��AG=PF=60��3t=BH��
��HQ=BQ��BH=20t����60��3t��=23t��60��
GQ=FQ��FG=BQ��AP=17t��
���ݹ��ɶ����ã�602=��17t��2����23t��60��2
��t1=4��t2=7.5���ᣩ��
��t=4
�����t=4��ʹAE=EF��
����������1���⣺��BP=BQʱ��60��3t=20t��
��t= ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫�������ڱ��⿼��ĵ��������ε����ʺ��ɶ����ĸ����Ҫ�˽���������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ˡ������������У�������������������ij������Ͻ���ڵ�һ�����Ϊ1000m2�Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի������ֲݲ��ֵ����Ϊx��m2�����ֲ��������y1��Ԫ����x��m2���ĺ�����ϵʽΪ ![]() ����ͼ����ͼ��ʾ���Ի��������y2��Ԫ����x��m2���ĺ�����ϵʽΪy2=��0.01x2��20x+30000��0��x��1000����
����ͼ����ͼ��ʾ���Ի��������y2��Ԫ����x��m2���ĺ�����ϵʽΪy2=��0.01x2��20x+30000��0��x��1000���� 
��1����ֱ��д��k1��k2��b��ֵ��
��2�������1000m2�յص��̻��ܷ���ΪW��Ԫ����������W��x�ĺ�����ϵʽ������̻��ܷ���W�����ֵ��
��3�����ֲݲ��ֵ����������700m2 �� �Ի����ֵ����������100m2 �� ������̻��ܷ���W����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BD��CE�ֱ�ΪAC��AB���ϵ����ߣ�BD��CE����BD=4��CE=6�����ABC�����Ϊ�� ��
A.12
B.24
C.16
D.32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ���DAC�͡�DBE���ǵȱ������Σ� 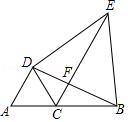
��1����֤����DAB�ա�DCE��
��2��BD��CE���ڵ�F������ADBΪ�۽ǣ��ڲ������κθ����ߵ�����£�ֱ��д��ͼ�����в���60������ȵ���ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���E��F�ֱ��ڱ�CD��BC�ϣ���DC=3DE=3a����������ֱ��EF�۵���ʹ��Cǡ������AD���ϵĵ�P������FP= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ŷֱ����������Ρ�ƽ���ı��Ρ�����ͼ���Ŀ�Ƭ�����dz�ͼ������ȫ��ͬ���ѿ�Ƭ���泯��ϴ�ȣ����������ȡһ�ź�Żأ��ٱ��泯��ϴ�ȣ����������ȡһ�ţ������γ����ÿһ�ſ�Ƭ��ͼ��������Գ�ͼ���������ĶԳ�ͼ�εĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ǰ��ij����������ӦƸ����˾��ŵ���ʴ�����ͼ��������С�ŷ��֣��ӹ�1��A�������3��B�������5Сʱ���ӹ�2��A�������5��B�������9Сʱ�� ���ʴ�����ÿ�¹�������3000Ԫ��ÿ�칤��8Сʱ��ÿ�¹���25�죬�ӹ�1��A������Ƴ�16Ԫ���ӹ�1��B������Ƴ�12Ԫ���¹���=��н��800Ԫ��+�Ƽ����ʣ�
��1��С�żӹ�1��A�������1��B���������Ҫ����Сʱ��
��2������˾�涨��С��ÿ�±���ӹ�A��B�����ͺŵ�������Ҽӹ�B�͵�����������A�����������2������С��ÿ�¼ӹ�A�����a���������ܶ�ΪWԪ������������ѧ֪ʶ�жϸù�˾�䲼ִ�д˹涨���Ƿ�Υ���˹��ʴ�����ŵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4��E��BC���ϵ�һ�����㣬AE��EF��EF��DC�ڵ�F����BE=x��FC=y����E�ӵ�B�˶�����Cʱ��y����x�ĺ���ͼ���ǣ� ��
A.
B.
C.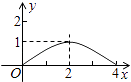
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�릤A��B��C������ֱ��l�Գƣ����B�Ķ���Ϊ ����
A.30��
B.50��
C.90��
D.100��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com