练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．计算：
    （1）$\frac{x+1}{x-1}$-$\frac{4x}{{x}^{2}-1}$；
    （2）（a+1-$\frac{3}{a-1}$）•$\frac{2a-2}{a+2}$．

    分析 （1）先把要求的式子进行通分，然后进行因式分解，最后约分即可；
    （2）先通分，再把分子进行因式分解，然后约分即可得出答案．

    解答 解：（1）$\frac{x+1}{x-1}$-$\frac{4x}{{x}^{2}-1}$=$\frac{（x+1）^{2}}{（x+1）（x-1）}$-$\frac{4x}{（x+1）（x-1）}$=$\frac{（x-1）^{2}}{（x+1）（x-1）}$=$\frac{x-1}{x+1}$．

    （2）（a+1-$\frac{3}{a-1}$）•$\frac{2a-2}{a+2}$=[$\frac{（a+1）（a-1）}{a-1}$-$\frac{3}{a-1}$]•$\frac{2（a-1）}{a+2}$=$\frac{（a+2）（a-2）}{a-1}$•$\frac{2（a-1）}{a+2}$=2a-4．

    点评 此题考查了分式的化简求值，分式的加减运算关键是通分，通分的关键是找最简公分母；分式的乘除运算关键是约分，约分的关键是找公因式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．计算：
    （1）（2m+n）（2m-n）-2（m-n）2
    （2）$\frac{{x}^{-2}-{y}^{-2}}{{x}^{-1}+{y}^{-1}}$
    （3）（$\frac{1}{a+1}$-$\frac{1}{1-a}$）•$\frac{a-1}{a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

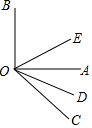    3．如图所示，已知∠AOB=90°，∠AOC为锐角，OD平分∠AOC，OE平分∠BOC．
    （1）求∠DOE的度数．
    （2）当∠AOB=m°时，∠DOE等于多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

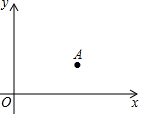    20．如图，点A的坐标为（3，2），点B与点A关于x轴对称，AB交x轴于点C．
    （1）在图中描出点B．井写出点C的坐标；
    （2）求△ABO的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，AB是半圆O的直径，射线AM、BN分别与半圆O相切于点A、B，点E在半圆上，点D在射线AM上，连接DE并延长交射线BN于点C，连接AE并延长交射线BN于点G．
    （1）若点C为BG的中点，求证：CD与⊙O相切；
    （2）在满足（1）的条件下，若AB=12，AD=x，BC=y．
    ①求y与x的函数关系式（不要求写出自变量的取值范围）；
    ②当x为何值时，四边形OBCE为正方形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知y与x成反比例，当x=4时，y=3．
    （1）求y与x的函数关系式；
    （2）当x=1时求y值；
    （3）当y=1时，求x值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

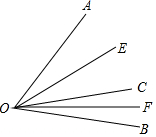    4．已知，如图，OC是∠AOB内部一条射线，∠AOB=60°，OE、OF分别是∠AOC、∠COB的角平分线，求∠EOF的度数？如果设∠AOB=β，其他条件不变，你能猜测出∠EOF的大小吗？请用一句简洁的话表述你发现的规律．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知a2-4a-3=0，求代数式3（a2-2a）-（a2+2a+1）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．绝对值大于1而小于4的整数有4个；已知点A在数轴上表示的数是-2，则与点A的距离等于3的点表示的数是-5或1．

    查看答案和解析>>

    同步练习册答案