
分析 (1)利用等边三角形的性质得∠B=∠C=∠A=60°,因为BD=BE=EC=CF=AF=AD,由等边三角形的判定得出∠1=∠2=∠3=60°,易得结论;
(2)利用(1)的结论即可得出答案;
(3)方法一:①由平行线的性质得∠BEF=∠BAC,由入射角等于反射角的结论得:∠BEF=∠AEH,等量代换得∠AEH=∠BAC,易得tan∠AEH=∠tan∠BAC,得出结论;②由等角对等边易得AJ=EJ,因为∠AEH+∠AHE=90°,∠EAC+∠ACB=90°,∠AEH=∠EAC,得∠AHE=∠ACB,由AD∥BC得∠ACB=∠CAD,∠CAD=∠AHE,所以AJ=HJ,同理FK=KC,GK=KC,EF=JK,HG=JK,得出结论;
方法二:①由(1)的结论得∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8,由平行线的性质得∠1=∠ACB,∠8=∠BAC,等量代换得∠AEH=∠BAC,得出结论;②由平行四边形的判定得四边形EFGH是平行四边形,设BE=3x,则BF=4x,EF=5x,易得FC=4-4x,$CG=\frac{3}{4}CF=3-3x$,DG=3=CG=3x,BE=DG=3x,由勾股定理得FG,四边形EFGH的周长为2(EF+FG,代入得四边形EFGH的周长.
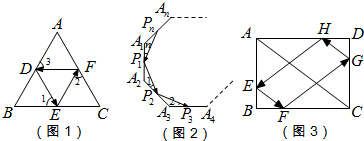
解答 解:(1)如图1,∵△ABC为等边三角形,点D、E、F分别是其三边的中点,
∴∠B=∠C=∠A=60°,BD=BE=EC=CF=AF=AD,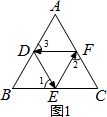
∴△BDE,△CEF,△ADF均为等边三角形,
∴∠1=∠2=∠3=60°
∴∠1+∠2+∠3=180°,
故答案为:180°;
(2)如图2,由(1)的结论可得:∠1+∠2+∠3+…∠n=180°,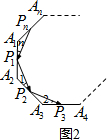
∴∠A2P2P1=$\frac{180°}{n}$,
故答案为:$\frac{180°}{n}$
(3)如图3,
方法一:①连结AC交EH,FG于点J,K,
∵EF∥AC
∴∠BEF=∠BAC,
由入射角等于反射角的结论得:∠BEF=∠AEH,
∴∠AEH=∠BAC
∴tan∠AEH=∠tan∠BAC=$\frac{4}{3}$;
②∵∠AEH=∠BAC,
∴AJ=EJ,
∵∠AEH+∠AHE=90°,∠EAC+∠ACB=90°,∠AEH=∠EAC,
∴∠AHE=∠ACB,
又∵AD∥BC,
∴∠ACB=∠CAD,
∴∠CAD=∠AHE,
∴AJ=HJ,
同理FK=KC,GK=KC,EF=JK,HG=JK,
∴LEFGH=HE+EF+FG+GH=2AJ+2KC+2JK=2AC=10,
∴四边形EFGH的周长为定值10;
方法二:①如图4,依据题意得∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8,
∵EF∥AC,
∴∠1=∠ACB,∠8=∠BAC,
∴∠7=∠BAC即∠AEH=∠BAC,
∴$tan∠AEH=tan∠BAC=\frac{BC}{AB}=\frac{4}{3}$;
②∵四边形ABCD是矩形,
∴∠CAD=∠AC,
又∵EF∥AC,
∴∠1=∠ACB,
∴∠1=∠CAD,
而∠1=∠2,∠3=∠4,且∠2+∠3=90°,
∴∠1+∠4=90°,
又∠4+∠5=90°,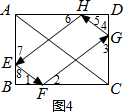
∴∠5=∠1,
∴∠5=∠CAD,
∴GH∥AC,
∴EF∥GH,
在Rt△EBF,Rt△FCG和Rt△GDH中,
设BE=3x,则BF=4x,EF=5x,
∴FC=4-4x,$CG=\frac{3}{4}CF=3-3x$,
∴DG=3=CG=3x,
∴BE=DG=3x,
又∵∠5=∠1,
∴△EBF≌△GDH,
∴EF=GH,
∴四边形EFGH是平行四边形,
又∵$FG=\sqrt{{{(3-3x)}^2}+{{(4-4x)}^2}}=5-5x$,
∴四边形EFGH的周长为2(EF+FG)=2(5x+5-5x)=10,
∴四边形EFGH的周长为定值10.
点评 本题主要考查了等边三角形的性质,平行四边形的判定,平行线的性质等,灵活运用结论,综合运用各种判定定理是解答此题的关键.


科目:初中数学 来源: 题型:选择题
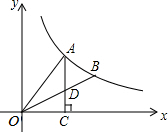 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角△ABC中,∠C=90゜.
如图,直角△ABC中,∠C=90゜.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
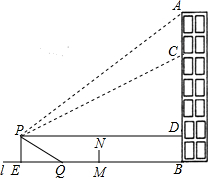 如图,重庆某广场新建与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直.在P处测得建筑物顶端A的仰角为37°,测得建筑物C处的仰角为26.6°(不计测量人员的身高),CD为25米.图中的点A、B、C、D、P及直线l均在同一平面内.
如图,重庆某广场新建与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直.在P处测得建筑物顶端A的仰角为37°,测得建筑物C处的仰角为26.6°(不计测量人员的身高),CD为25米.图中的点A、B、C、D、P及直线l均在同一平面内.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤0 | B. | x≠-1 | C. | x≤0且x≠-1 | D. | x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
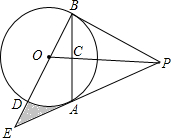 如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com