
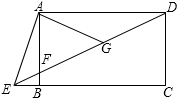
 如图,四边形ABCD是长方形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠ADE,点G是DF的中点,若BE=1,AG=3,则AB的长为2$\sqrt{2}$.
如图,四边形ABCD是长方形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠ADE,点G是DF的中点,若BE=1,AG=3,则AB的长为2$\sqrt{2}$. 分析 根据直角三角形斜边上的中线等于斜边的一半可得AG=DG,然后根据等边对等角的性质可得∠ADG=∠DAG,再结合两直线平行,内错角相等可得∠ADG=∠CED,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGE=2∠ADG,从而得到∠AED=∠AGE,再利用等角对等边的性质得到AE=AG,然后利用勾股定理列式计算即可得解.
解答 解:∵四边形ABCD是矩形,点G是DF的中点,
∴AG=DG,
∴∠ADG=∠DAG,
∵AD∥BC,
∴∠ADG=∠CED,
∴∠AGE=∠ADG+∠DAG=2∠CED,
∵∠AED=2∠ADE
∴∠AED=∠AGE,
∴AE=AG=3,
在Rt△ABE中,AB=$\sqrt{{AE}^{2}{-BE}^{2}}$=2$\sqrt{2}$.
点评 本题考查了矩形的性质,等边对等角的性质,等角对等边的性质,以及勾股定理的应用,求出AE=AG是解题的关键.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
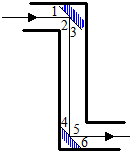 如图所示,潜望镜的两个镜子是平行放置的,光线经过镜子反射后,有∠1=∠3,∠4=∠6,请你解释为什么进入潜望镜的光线和离开潜望镜的光线也是平行的?
如图所示,潜望镜的两个镜子是平行放置的,光线经过镜子反射后,有∠1=∠3,∠4=∠6,请你解释为什么进入潜望镜的光线和离开潜望镜的光线也是平行的?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
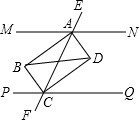 已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${x^2}+3x-4=x({x+3-\frac{4}{x}})$ | B. | (x+2)(x-2)=x2-4 | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | $-{x^2}+x-\frac{1}{4}=-{({x-\frac{1}{2}})^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{11}{3}$ | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
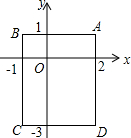 如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).
如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
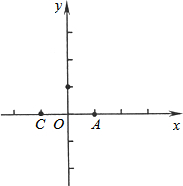 在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).
在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com