
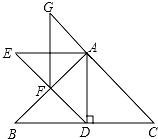
 如图,等腰角直角△ABC的直角边长为2,以它的斜边上的高AD为腰作第一个等腰直角△ADE;再以所作的第一个等腰直角△ADE的斜边上的高AF为腰作第二个等腰直角AFG…以此类推,这样所作的第n个等腰直角三角形的面积为$\frac{1}{{2}^{n}}$.
如图,等腰角直角△ABC的直角边长为2,以它的斜边上的高AD为腰作第一个等腰直角△ADE;再以所作的第一个等腰直角△ADE的斜边上的高AF为腰作第二个等腰直角AFG…以此类推,这样所作的第n个等腰直角三角形的面积为$\frac{1}{{2}^{n}}$. 分析 通过直角三角形的性质特点,斜边上的高等于斜边的一半,再分析规律,便能计算出答案了.
解答 解:∵等腰直角△ABC直角边长为2,
∴斜边长为=2$\sqrt{2}$.,
斜边上的高也是斜边上的中线,应该等于斜边的一半.
那么第一个等腰直角三角形的腰长为$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$;
∴第二个等腰直角三角形的斜边长=$\sqrt{2×(\sqrt{2})^{2}}$=2,
∴第二个等腰直角三角形的腰长=$\frac{1}{2}$×2=1,
那么第n个等腰直角三角形的腰长为($\frac{\sqrt{2}}{2}$)n-1.
∴第n个等腰直角三角形的面积=$\frac{1}{2}$×[($\frac{\sqrt{2}}{2}$)n-1]2=$\frac{1}{{2}^{n}}$,
故答案是:$\frac{1}{{2}^{n}}$.
点评 此题考查了等腰直角三角形,解决本题的关键是根据等腰直角三角形的性质得到其他等腰直角三角形的表示规律.


科目:初中数学 来源: 题型:选择题
| A. | x2+3y2+6x-9=0 | B. | x2+3y2-6x-9=0 | C. | x2+y2-2x-3=0 | D. | x2+y2+2x-3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com