
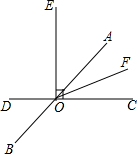
 如图所示,直线AB,CD相交于点O,OF平分∠AOC,EO⊥CD于点O,且∠DOF=160°,求∠BOE的度数.
如图所示,直线AB,CD相交于点O,OF平分∠AOC,EO⊥CD于点O,且∠DOF=160°,求∠BOE的度数. 分析 根据邻补角定义,可得∠COF=180°-∠DOF=20°,根据角平分线定义可得∠AOC=2∠COF=40°,根据对顶角相等得出∠DOB=∠AOC=40°,根据垂直的定义可得∠DOE=90°,那么∠BOE=∠DOE+∠DOB=130°.
解答 解:∵∠DOF+∠COF=180°,∠DOF=160°,
∴∠COF=180°-∠DOF=180°-160°=20°.
∵OF平分∠AOC,
∴∠AOC=2∠COF=40°,
∴∠DOB=∠AOC=40°.
∵EO⊥CD,
∴∠DOE=90°,
∴∠BOE=∠DOE+∠DOB=90°+40°=130°.
点评 本题考查了垂线,邻补角定义,角平分线定义,对顶角相等的性质.求出∠DOE与∠DOB的度数是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
 一次函数y=-x+1(0≤x≤10)与反比例函数y=$\frac{1}{x}$(-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1,y1),(x2,y2)是图象上两个不同的点,若y1=y2,则x1+x2的取值范围是( )
一次函数y=-x+1(0≤x≤10)与反比例函数y=$\frac{1}{x}$(-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1,y1),(x2,y2)是图象上两个不同的点,若y1=y2,则x1+x2的取值范围是( )| A. | -$\frac{89}{10}$≤x≤1 | B. | -$\frac{89}{10}$≤x≤$\frac{89}{9}$ | C. | -$\frac{89}{9}$≤x≤$\frac{89}{10}$ | D. | 1≤x≤$\frac{89}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
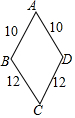 如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )
如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )| A. | 0<x<20 | B. | 2<x<20 | C. | 0<x<24 | D. | 2<x<24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com