
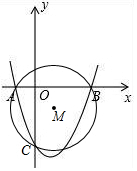
 如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.⊙M过A、B、C三点,P是抛物线上一点,连接PA,当PA与⊙M相切时,求点P的坐标.
如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.⊙M过A、B、C三点,P是抛物线上一点,连接PA,当PA与⊙M相切时,求点P的坐标. 分析 连接AM,过M作MN⊥AB于M,过P作PH⊥x轴于H,由AP是⊙M的切线,得到AM⊥AP,根据相似三角形的性质得到$\frac{AN}{PH}=\frac{MN}{AH}$,于是得到结论.
解答  解:连接AM,过M作MN⊥AB于M,过P作PH⊥x轴于H,
解:连接AM,过M作MN⊥AB于M,过P作PH⊥x轴于H,
∵AP是⊙M的切线,
∴AM⊥AP,
∴∠MAN+∠PAN=∠PAN+∠APH=90°,
∴∠MAN=∠APH,
∴△AMN∽△PHA,
∴$\frac{AN}{PH}=\frac{MN}{AH}$,
∵M(1,-1),
设P(m,m2-2m-3),
∴$\frac{2}{{m}^{2}-2m-3}$=$\frac{1}{m+1}$,
∴m=5,m=-1(舍去),
∴P(5,12).
点评 本题考查了切线的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
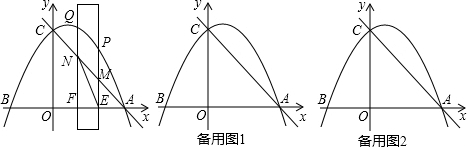
 如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.
如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对一批LED节能灯使用寿命的调查 | |
| B. | 对冷饮市场上冰淇淋质量情况的调查 | |
| C. | 对一个社区每天丢弃塑料袋数量的调查 | |
| D. | 对大型民用直升机各零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
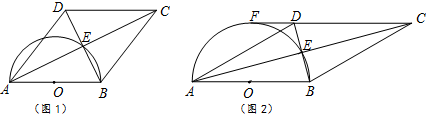
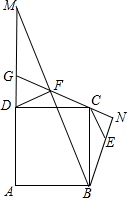 如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.
如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
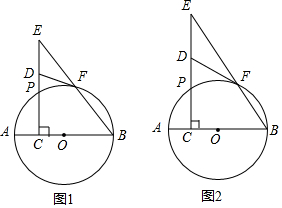
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com